Zadanie nr 1844851
Pole obszaru ograniczonego wykresem funkcji 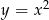 dla
dla 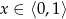 i osią
i osią 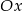 możemy obliczyć z dowolną dokładnością, zwiększając liczbę
możemy obliczyć z dowolną dokładnością, zwiększając liczbę  prostokątów o szerokości
prostokątów o szerokości 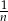 każdy (patrz rysunek) i sumując ich pola.
każdy (patrz rysunek) i sumując ich pola.
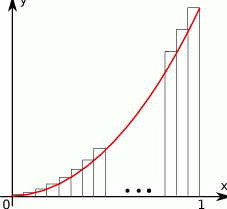
- Przedstaw ilustrację graficzną takiej sytuacji dla
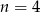 i oblicz sumę pól otrzymanych prostokątów.
i oblicz sumę pól otrzymanych prostokątów. 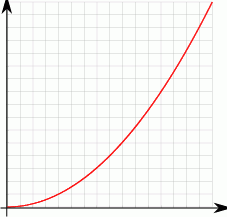
- Oblicz sumę
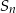 pól
pól  prostokątów, wykorzystując wzór:
prostokątów, wykorzystując wzór: 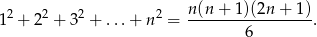
Rozwiązanie
- Prostokąty zaznaczone są na rysunku.
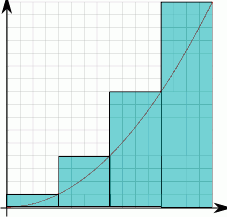
Każdy z nich ma poziomy bok długości
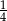 , zatem suma ich pól wynosi
, zatem suma ich pól wynosi 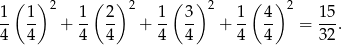
Odpowiedź: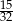
- Analogicznie jak w poprzednim punkcie, jeżeli będzie
 prostokątów, to ich pole będzie równe
prostokątów, to ich pole będzie równe 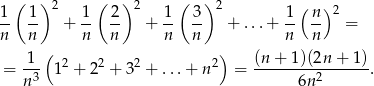
Na końcu skorzystaliśmy ze wzoru podanego w treści zadania.
Odpowiedź: