Zadanie nr 2016042
Wykres funkcji kwadratowej 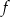 jest styczny do prostej
jest styczny do prostej 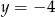 , przechodzi przez punkt
, przechodzi przez punkt 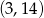 oraz jest symetryczny względem osi
oraz jest symetryczny względem osi 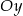 .
.
- Wyznacz wzór funkcji
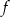 i narysuj jej wykres.
i narysuj jej wykres. - Rozwiąż nierówność
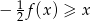
Rozwiązanie
- Szukamy funkcji postaci
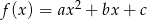 . Symetryczność względem osi
. Symetryczność względem osi 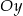 oznacza, że
oznacza, że 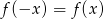 , czyli
, czyli 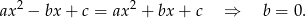
Fakt, że wykres tej funkcji jest styczny do prostej
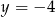 oznacza, że druga współrzędna wierzchołka tej paraboli jest równa
oznacza, że druga współrzędna wierzchołka tej paraboli jest równa 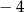 . Zatem
. Zatem 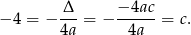
Pozostało skorzystać z informacji o tym, że punkt
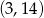 należy do wykresu.
należy do wykresu. 
Odpowiedź: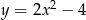
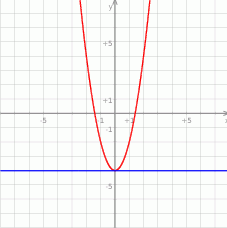
- Zobaczmy jak wygląda podana nierówność
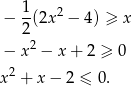
Liczymy,
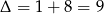 ,
, 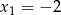 ,
, 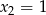 . Stąd
. Stąd 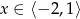 .
.
Odpowiedź: