Zadanie nr 2181749
Dany jest wykres funkcji kwadratowej 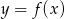
- Korzystając z danych na wykresie wyznacz wzór funkcji
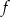 w postaci ogólnej.
w postaci ogólnej. - Oblicz współrzędne wierzchołka paraboli.
- Podaj zbiór rozwiązań nierówności
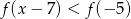 .
.
Rozwiązanie
- Ponieważ liczby
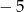 i
i 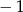 są miejscami zerowymi tego trójmianu, ma on postać
są miejscami zerowymi tego trójmianu, ma on postać 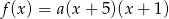 . Współczynnik
. Współczynnik  wyliczamy z faktu, że
wyliczamy z faktu, że 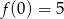 .
. 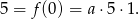
A zatem
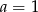 , skąd
, skąd 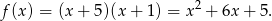
Odpowiedź: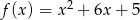
- Liczymy
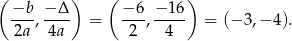
Odpowiedź: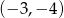
- Ponieważ
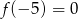 , oraz wiemy,
, oraz wiemy, 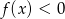 dla
dla 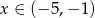 (z wykresu), to dana nierówność sprowadza się do
(z wykresu), to dana nierówność sprowadza się do 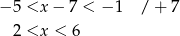
Odpowiedź: