Zadanie nr 5329338
Funkcja kwadratowa 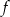 , której miejscami zerowymi są liczby
, której miejscami zerowymi są liczby 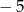 i 7, dla argumentu 1 przyjmuje wartość
i 7, dla argumentu 1 przyjmuje wartość 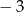 . Uzasadnij, że wykres funkcji
. Uzasadnij, że wykres funkcji 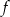 ma dwa punkty wspólne z prostą
ma dwa punkty wspólne z prostą 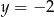 .
.
Rozwiązanie
Sposób I
Wykresem funkcji 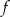 jest parabola. Wierzchołek tej paraboli leży dokładnie w środku między pierwiastkami, więc jego pierwsza współrzędna jest równa
jest parabola. Wierzchołek tej paraboli leży dokładnie w środku między pierwiastkami, więc jego pierwsza współrzędna jest równa
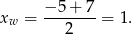
Druga współrzędna jest więc równa
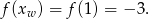
Ponieważ wierzchołek leży poniżej osi 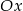 i wiemy, że parabola przecina tę oś, więc parabola ta ma ramiona skierowane w górę.
i wiemy, że parabola przecina tę oś, więc parabola ta ma ramiona skierowane w górę.
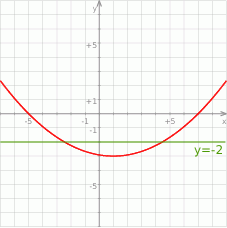
Ponadto 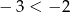 , więc rzeczywiście parabola
, więc rzeczywiście parabola 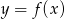 przecina prostą
przecina prostą 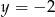 w dwóch punktach.
w dwóch punktach.
Sposób II
Z podanych miejsc zerowych wiemy, że funkcja 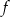 ma postać
ma postać
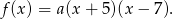
Współczynnik  wyznaczamy z warunku
wyznaczamy z warunku 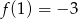 .
.
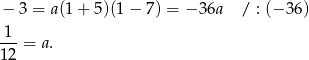
Zatem 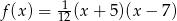 .
.
Wystarczy teraz udowodnić, że równanie 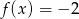 ma dwa rozwiązania.
ma dwa rozwiązania.
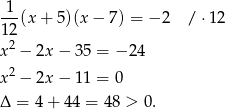
Ponieważ 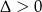 , powyższe równanie rzeczywiście ma dwa rozwiązania.
, powyższe równanie rzeczywiście ma dwa rozwiązania.

