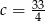/Szkoła średnia/Funkcje - wykresy/Parabola

Zadanie nr 7295605

Dodaj do ulubionych
Dodaj do rozwiązanych

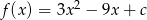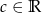Funkcja f określona jest wzorem 2 f(x ) = 3x − 9x + c , gdzie c ∈ R . Wyznacz wszystkie wartości współczynnika c , dla których:

  • jednym z miejsc zerowych funkcji 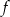f jest liczba 2;
  • wierzchołek paraboli, która jest wykresem funkcji 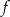f , należy do prostej o równaniu y = x .

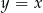Rozwiązanie

  • Liczymy kiedy 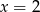x = 2 jest pierwiastkiem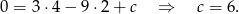
    0 = 3⋅4 − 9 ⋅2 + c ⇒ c = 6.

     
    Odpowiedź: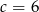 c = 6

  • Pierwsza współrzędna wierzchołka danej funkcji jest równa
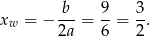
    -b- 9- 3- xw = − 2a = 6 = 2.

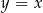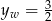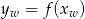    Skoro wierzchołek ma leżeć na prostej y = x , to musi być 3 yw = 2 . Ale yw = f(xw ) , co daje równanie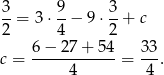

    3-= 3 ⋅ 9-− 9 ⋅ 3-+ c 2 4 2 6− 27+ 54 33 c = ------------= --. 4 4

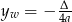    Oczywiście mogliśmy też to samo wyliczyć ze wzoru Δ yw = − 4a .  
    Odpowiedź: c = 343

Wersja PDF