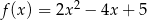/Szkoła średnia/Funkcje - wykresy/Parabola

Zadanie nr 7849007

Dodaj do ulubionych
Dodaj do rozwiązanych

Dana jest funkcja kwadratowa określona wzorem 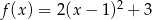2 f(x ) = 2(x − 1) + 3 .

  • podaj współrzędne wierzchołka paraboli będącej wykresem tej funkcji.
  • podaj zbiór wartości tej funkcji.
  • podaj równanie osi symetrii paraboli będącej wykresem tej funkcji.
  • podaj wzór tej funkcji w postaci ogólnej.

Rozwiązanie

Naszkicujmy parabolę będącą wykresem funkcji 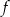f – jest to parabola 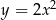y = 2x2 przesunięta o jedną jednostkę w prawo i trzy jednostki w górę.

PIC

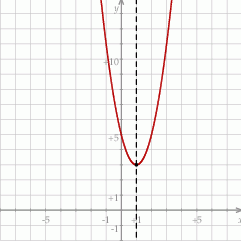
  • Współrzędne wierzchołka odczytujemy wprost z postaci kanonicznej.
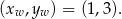
    (xw ,yw) = (1,3 ).

     
    Odpowiedź: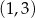 (1,3)

  • Ponieważ ramiona paraboli będącej wykresem funkcji 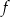f są skierowane w górę, to zbiorem wartości tej funkcji jest przedział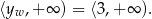
    ⟨yw ,+∞ ) = ⟨3,+ ∞ ).

     
    Odpowiedź: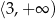 ⟨3 ,+ ∞ )

  • Osią symetrii tej paraboli jest pionowa prosta przechodząca przez jej wierzchołek, czyli prosta x = 1 .  
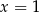    Odpowiedź: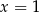 x = 1
  • Przekształcamy podany wzór funkcji f
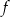
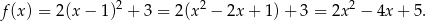
    f(x ) = 2(x − 1)2 + 3 = 2(x 2 − 2x + 1)+ 3 = 2x2 − 4x + 5.

     
    Odpowiedź: 2 f(x ) = 2x − 4x + 5

Wersja PDF