Zadanie nr 8925296
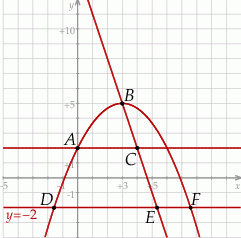
Na rysunku przedstawiono fragmenty wykresów funkcji kwadratowej oraz trzech funkcji liniowych. Zaznaczono również niektóre punkty szczególne tych wykresów: 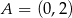 ,
, 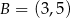 i
i 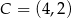 . Wyznacz współrzędne punktów
. Wyznacz współrzędne punktów 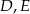 i
i 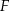 .
.
Rozwiązanie
Wiemy, że wierzchołkiem narysowanej paraboli jest punkt 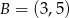 , więc ma on wzór postaci
, więc ma on wzór postaci
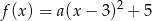
(postać kanoniczna). Współczynnik  wyznaczamy podstawiając współrzędne punktu
wyznaczamy podstawiając współrzędne punktu 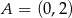 .
.
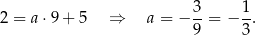
Zatem
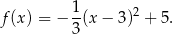
To pozwala już wyznaczyć współrzędne punktów 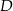 i
i 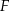 – rozwiązujemy równanie kwadratowe
– rozwiązujemy równanie kwadratowe
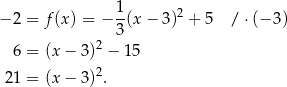
Stąd
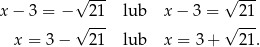
i 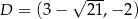 ,
, 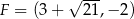 .
.
Teraz zajmijmy się punktem 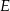 . Najpierw napiszmy równanie prostej
. Najpierw napiszmy równanie prostej 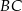 – szukamy prostej w postaci
– szukamy prostej w postaci 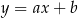 i podstawiamy współrzędne punktów
i podstawiamy współrzędne punktów 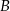 i
i 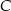 .
.
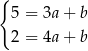
Odejmujemy od drugiego równania pierwsze i mamy 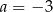 . Stąd
. Stąd 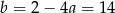 i prosta ta ma równanie
i prosta ta ma równanie 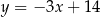 . Szukamy teraz jej punktu wspólnego
. Szukamy teraz jej punktu wspólnego 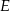 z prostą
z prostą 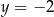 – podstawiamy
– podstawiamy 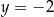 .
.
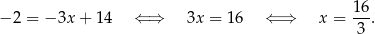
Zatem 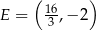 .
.
Odpowiedź: 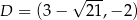 ,
, 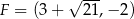 ,
,