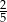Zadanie nr 9567395
Suma dziewięciu początkowych wyrazów ciągu arytmetycznego wynosi 18, a suma siedmiu początkowych wyrazów jest równa 0. Wyrazy: siódmy, ósmy i dziewiąty są długościami boków trójkąta. Oblicz stosunek długości promienia okręgu wpisanego w ten trójkąt do długości promienia okręgu na nim opisanego.
Rozwiązanie
Ze wzoru na sumę początkowych wyrazów ciągu arytmetycznego mamy układ równań
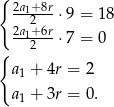
Odejmując od pierwszego równania drugie, mamy 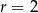 , czyli
, czyli 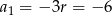 . Możemy teraz obliczyć:
. Możemy teraz obliczyć: 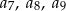 .
.
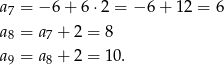
Mamy zatem trójkąt o bokach 6, 8, 10. Jest on dwa razy większy od trójkąta o bokach 3, 4, 5, więc łatwo zgadnąć (i sprawdzić z twierdzenia Pitagorasa), że mamy do czynienia z trójkątem prostokątnym.
Promień okręgu opisanego na trójkącie prostokątnym to dokładnie połowa przeciwprostokątnej, czyli 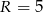 . Promień okręgu wpisanego obliczamy ze wzoru na pole
. Promień okręgu wpisanego obliczamy ze wzoru na pole 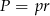 , gdzie
, gdzie
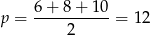
jest połową obwodu. Mamy więc
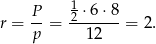
Zatem szukany iloraz jest równy 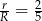 .
.
Odpowiedź: