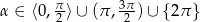Zadanie nr 6240592
Dany jest ciąg geometryczny 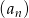 o wyrazie ogólnym
o wyrazie ogólnym 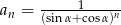 , gdzie
, gdzie 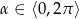 . Dla jakich wartości
. Dla jakich wartości  ciąg
ciąg 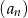 jest zbieżny?
jest zbieżny?
Rozwiązanie
Ciąg geometryczny o ilorazie 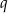 jest zbieżny jeżeli
jest zbieżny jeżeli 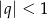 lub
lub 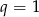 . Zanim ustalimy kiedy tak będzie przekształćmy
. Zanim ustalimy kiedy tak będzie przekształćmy 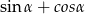 .
.
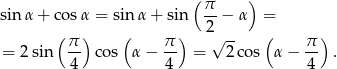
Mamy w szczególności
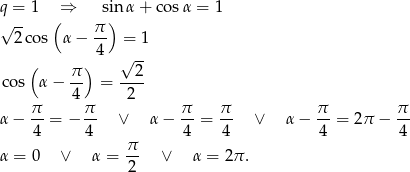
Mamy jeszcze nierówność
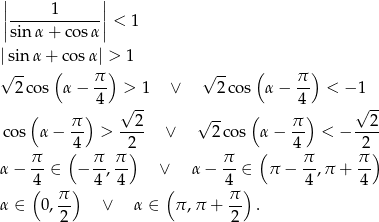
Odpowiedź: