/Szkoła średnia/Ciągi/Arytmetyczny/W geometrii/Trójkąt prostokątny

Zadanie nr 3357050

Dodaj do ulubionych
Dodaj do rozwiązanych

W trójkącie prostokątnym jedna z przyprostokątnych jest średnią arytmetyczną drugiej przyprostokątnej i przeciwprostokątnej. Oblicz sinusy kątów ostrych tego trójkąta.

Rozwiązanie

Szkicujemy trójkąt prostokątny.

PIC

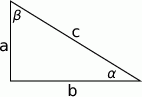
Możemy tak oznaczyć boki trójkąta aby podany warunek zapisać w postaci: 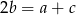2b = a+ c .

Sposób I

Podnosząc równośc 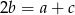2b = a + c do kwadratu i stosując twierdzenie Pitagorasa mamy

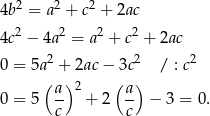
4b2 = a2 + c2 + 2ac 4c2 − 4a 2 = a2 + c2 + 2ac 2 2 2 0 = 5a + 2ac − 3c / : c ( a) 2 ( a) 0 = 5 c + 2 c − 3 = 0.

Podstawiając 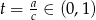t = a ∈ (0,1) c mamy równanie

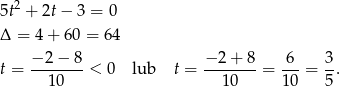
5t2 + 2t − 3 = 0 Δ = 4+ 60 = 64 −-2-−-8 −-2+--8 -6- 3- t = 1 0 < 0 lub t = 10 = 10 = 5 .

Stąd

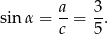
sin α = a-= 3-. c 5

Zatem

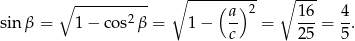
∘ ---------- ∘ ----(--)-2 ∘ --- sin β = 1 − cos2β = 1 − a- = 1-6 = 4-. c 2 5 5

Sposób II

Piszemy i przekształcamy twierdzenie Pitagorasa

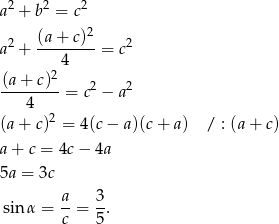
a2 + b2 = c2 2 (a+--c)2 2 a + 4 = c 2 (a-+-c)- = c2 − a2 4 (a+ c)2 = 4(c− a)(c+ a) / : (a + c) a+ c = 4c− 4a 5a = 3c sin α = a-= 3. c 5

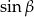sin β wyliczamy jak w sposobie I.

Sposób III

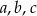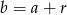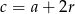Skoro a,b,c tworzą ciąg arytmetyczny, to b = a + r i c = a + 2r . Piszemy teraz twierdzenie Pitagorasa.

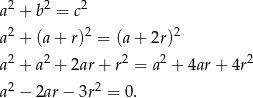
2 2 2 a + b = c a2 + (a + r)2 = (a + 2r)2 2 2 2 2 2 a + a + 2ar + r = a + 4ar + 4r a2 − 2ar − 3r 2 = 0.

Traktujemy otrzymaną równość jak równanie kwadratowe z niewiadomą a i parametrem r .

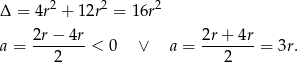
2 2 2 Δ = 4r + 12r = 16r 2r-−-4r 2r-+-4r a = 2 < 0 ∨ a = 2 = 3r.

Oczywiście pierwsze rozwiązanie odrzucamy i mamy 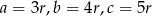a = 3r,b = 4r,c = 5r . Stąd

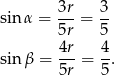
3r- 3- sin α = 5r = 5 4r 4 sin β = ---= -. 5r 5

 
Odpowiedź: 35 i 45

Wersja PDF