/Szkoła średnia/Ciągi/Arytmetyczny/W geometrii/Trójkąt prostokątny

Zadanie nr 8937296

Długości boków trójkąta prostokątnego tworzą ciąg arytmetyczny. Najkrótszy bok ma długość 6 cm. Oblicz

  • pole tego trójkata;
  • długość promienia okręgu opisanego na trójkącie;
  • długość promienia okręgu wpisanego w trójkąt.
Wersja PDF

Rozwiązanie

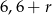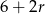  • Obliczymy najpierw boki trójkąta. Z podanych danych wynika, że boki mają długości 6,6 + r i 6 + 2r dla pewnego 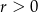r > 0 . Na mocy twierdzenia Pitagorasa mamy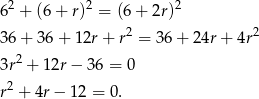
    62 + (6+ r)2 = (6+ 2r)2 36 + 36 + 12r + r2 = 36 + 24r + 4r2 2 3r + 12r− 36 = 0 r2 + 4r− 1 2 = 0.

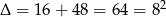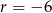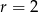    Rozwiązujemy to równanie kwadratowe. Δ = 16+ 48 = 64 = 82 , r = − 6 lub r = 2 . Rozwiązanie ujemne odrzucamy, zatem boki trójkąta to 6, 8 i 10, a jego pole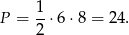

    1 P = -⋅ 6⋅8 = 24. 2

     
    Odpowiedź: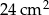 24 cm 2

  • Ponieważ średnicą okręgu opisanego na trójkącie prostokątnym jest przeciwprostokątna, to
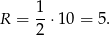
    R = 1-⋅10 = 5 . 2

    Mogliśmy też skorzystać ze wzoru na pole trójkąta 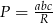abc P = R , który łatwo wynika z twierdzenia sinusów.  
    Odpowiedź: 5 cm

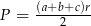  • Korzystamy ze wzoru na pole trójkąta P = (a+b-+c)r 2 .
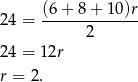
    (6+--8+--10)r- 24 = 2 24 = 12r r = 2.

     
    Odpowiedź: 2 cm

Wersja PDF