Zadanie nr 7014817
Liczby 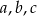 mają tę własność, że każdy z ciągów:
mają tę własność, że każdy z ciągów: 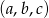 ,
, 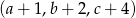 i
i 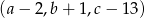 jest ciągiem geometrycznym. Oblicz
jest ciągiem geometrycznym. Oblicz 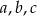 .
.
Rozwiązanie
Podane informacje prowadzą do układu równań
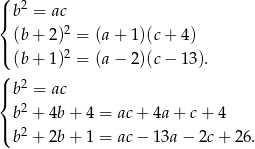
Odejmujemy teraz od drugiego i trzeciego równania pierwsze.
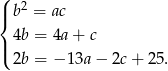
Teraz do trzeciego równania dodajemy drugie pomnożone przez 2 (żeby skrócić w nim  ).
).
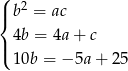
Z trzeciego równania mamy więc 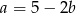 . Podstawiamy to wyrażenie w dwóch pierwszych równaniach.
. Podstawiamy to wyrażenie w dwóch pierwszych równaniach.
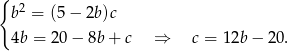
Podstawiamy teraz obliczone wyrażenie na  z drugiego równania do pierwszego.
z drugiego równania do pierwszego.
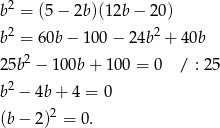
Zatem 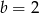 ,
, 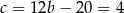 i
i 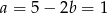 .
.
Odpowiedź: