Zadanie nr 8797003
Funkcje 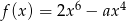 ,
, 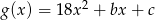 i
i 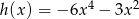 mają tę własność, że dla każdej liczby rzeczywistej
mają tę własność, że dla każdej liczby rzeczywistej 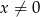 , liczby
, liczby 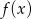 ,
, 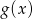 i
i 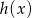 tworzą (w pewnej ustalonej kolejności) ciąg geometryczny. Wykaż, że funkcja
tworzą (w pewnej ustalonej kolejności) ciąg geometryczny. Wykaż, że funkcja 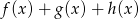 jest rosnąca na przedziale
jest rosnąca na przedziale 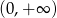 .
.
Rozwiązanie
Pierwszą rzeczą, którą musimy zrobić, to ustalić w jakiej kolejności liczby te mogą tworzyć ciąg geometryczny. Patrzymy na najwyższe potęgi  w podanych wielomianach. Ponieważ kwadrat jednej z tych potęg musi być iloczynem dwóch pozostałych, środkowym wyrazem ciągu musi być
w podanych wielomianach. Ponieważ kwadrat jednej z tych potęg musi być iloczynem dwóch pozostałych, środkowym wyrazem ciągu musi być 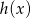 i
i
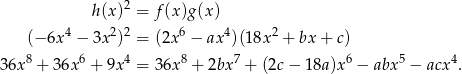
Mamy zatem
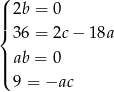
Stąd 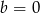 i
i 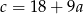 . Podstawiamy tę wartość do ostatniego równania.
. Podstawiamy tę wartość do ostatniego równania.
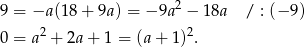
Zatem 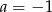 ,
, 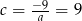 i
i
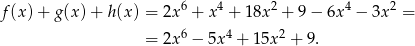
Musimy jeszcze wykazać, że funkcja ta jest rosnąca dla 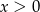 . Żeby uprościć rachunki podstawiamy
. Żeby uprościć rachunki podstawiamy 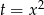 i rozważamy funkcję
i rozważamy funkcję
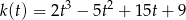
określoną dla 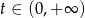 . Liczymy pochodną
. Liczymy pochodną
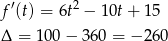
Ponieważ 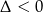 , pochodna jest dodatnia dla
, pochodna jest dodatnia dla 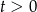 , czyli funkcja
, czyli funkcja 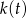 jest rosnąca na przedziale
jest rosnąca na przedziale 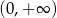 .
.

