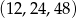Zadanie nr 8803571

Wyznacz trzywyrazowy ciąg geometryczny, w którym suma trzech kolejnych wyrazów jest równa 84, a ich iloczyn jest równy 13824.

Wersja PDF

Rozwiązanie

Sposób I

Jeżeli trzy liczby tworzą ciąg geometryczny, to są one postaci 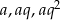2 a,aq,aq . Mamy zatem układ równań

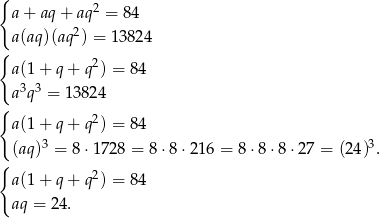
{ a+ aq+ aq2 = 84 a(aq)(aq2) = 13 824 { a(1+ q+ q2) = 84 3 3 a q = 1382 4 { 2 a(1+ q+ q ) = 84 (aq)3 = 8 ⋅1728 = 8 ⋅8 ⋅216 = 8⋅8 ⋅8 ⋅27 = (24 )3. { a(1+ q+ q2) = 84 aq = 24.

Podstawiamy 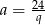24 a = q z drugiego równania do pierwszego. Prowadzi to do równania

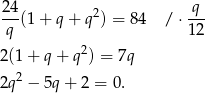
24-(1+ q+ q 2) = 84 / ⋅ q-- q 12 2 2(1 + q + q ) = 7q 2q2 − 5q + 2 = 0.

Rozwiązujemy to równanie kwadratowe, 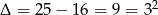Δ = 25 − 16 = 9 = 32 ,

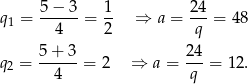
q = 5−-3-= 1- ⇒ a = 24-= 48 1 4 2 q 5 + 3 2 4 q2 = ------= 2 ⇒ a = --- = 12. 4 q

Mamy zatem dwa ciągi

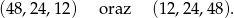
(48,24,12 ) oraz (12,24,48).

Sposób II

Szukamy trzech liczb 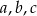a,b,c spełniających warunki

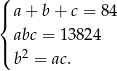
( |{ a+ b+ c = 84 abc = 138 24 |( 2 b = ac.

Podstawiamy 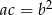2 ac = b z trzeciego równania do drugiego.

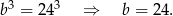
3 3 b = 24 ⇒ b = 24.

Mamy więc układ równań

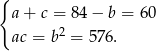
{ a + c = 84 − b = 6 0 2 ac = b = 5 76.

Podstawiamy 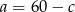a = 60− c z pierwszego równania do drugiego.

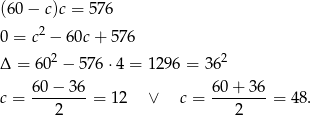
(60− c)c = 576 0 = c2 − 60c+ 576 Δ = 6 02 − 5 76⋅ 4 = 1296 = 362 60 − 36 60+ 36 c = --------= 12 ∨ c = --------= 4 8. 2 2

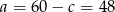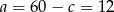Mamy wtedy a = 60 − c = 48 i a = 60 − c = 12 odpowiednio.
Odpowiedź: 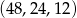(48,24 ,12) oraz (12,24,48)