Zadanie nr 3074601
Niech 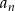 , dla
, dla 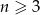 będzie liczbą krawędzi graniastosłupa prostego o podstawie będącej
będzie liczbą krawędzi graniastosłupa prostego o podstawie będącej  -kątem foremnym.
-kątem foremnym.
- Wyznacz wzór ciągu
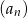 .
. - Sprawdź czy ciąg
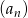 jest ciągiem arytmetycznym.
jest ciągiem arytmetycznym. - Uzasadnij, że żaden wyraz tego ciągu nie jest równy 2009.
Rozwiązanie
- Szkicujemy sobie taki graniastosłup.
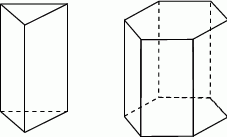
Widać, że ma on
 krawędzi w podstawie,
krawędzi w podstawie,  w drugiej podstawie i
w drugiej podstawie i  krawędzi bocznych. Mamy więc
krawędzi bocznych. Mamy więc 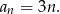
Odpowiedź: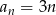 dla
dla 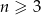
- Musimy sprawdzić, czy różnica kolejnych wyrazów nie zależy od
 (jest stała). Liczymy
(jest stała). Liczymy 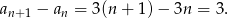
Różnica jest stała, więc ciąg jest arytmetyczny.
Odpowiedź: Tak, jest arytmetyczny. - Ze wzoru
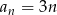 wynika, że każdy wyraz ciągu
wynika, że każdy wyraz ciągu 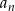 dzieli się przez 3. Tymczasem 2009 nie dzieli się przez 3 (bo suma cyfr jest równa 11).
dzieli się przez 3. Tymczasem 2009 nie dzieli się przez 3 (bo suma cyfr jest równa 11).

