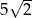Zadanie nr 8442905
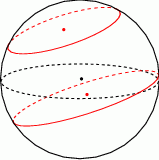
Kulę o promieniu  przecięto dwiema równoległymi płaszczyznami w sposób przedstawiony na poniższym rysunku. Przekroje mają promienie
przecięto dwiema równoległymi płaszczyznami w sposób przedstawiony na poniższym rysunku. Przekroje mają promienie  oraz
oraz  i są odległe od siebie o
i są odległe od siebie o  . Liczby
. Liczby 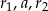 w podanej kolejności tworzą trzywyrazowy ciąg arytmetyczny, którego różnica jest równa 1. Suma wyrazów tego ciągu jest równa 18. Znajdź długość promienia kuli.
w podanej kolejności tworzą trzywyrazowy ciąg arytmetyczny, którego różnica jest równa 1. Suma wyrazów tego ciągu jest równa 18. Znajdź długość promienia kuli.
Rozwiązanie
Zajmijmy się najpierw informacją o ciągu arytmetycznym. Wiemy, że 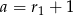 i
i 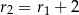 . Znamy też sumę tych liczb
. Znamy też sumę tych liczb
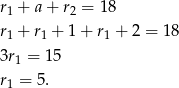
Zatem 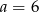 i
i 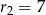 .
.
Narysujmy teraz przekrój kuli płaszczyzną przechodzącą przez środki przekrojów.
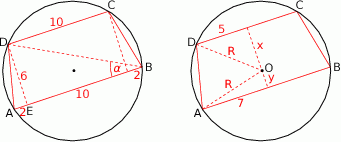
Widać, że mamy do czynienia z trapezem wpisanym w okrąg (trapez jest więc równoramienny), w którym znamy długości podstaw i długość wysokości.
Sposób I
Promień okręgu opisanego na trapezie możemy obliczyć z twierdzenia sinusów w trójkącie 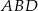 . Liczymy
. Liczymy
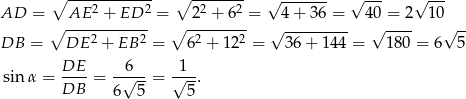
Korzystamy teraz z twierdzenia sinusów.
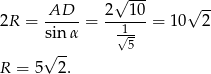
Sposób II
Tym razem objedziemy się bez twierdzenia sinusów. Połączmy środek okręgu opisanego na trapezie  z wierzchołkami
z wierzchołkami 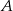 i
i 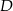 oraz niech
oraz niech  i
i 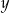 będą odległościami tego punktu od podstaw trapezu. Na mocy twierdzenia Pitagorasa mamy układ równań
będą odległościami tego punktu od podstaw trapezu. Na mocy twierdzenia Pitagorasa mamy układ równań
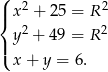
Podstawiamy 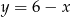 z trzeciego równania do drugiego i mamy
z trzeciego równania do drugiego i mamy
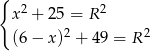
Odejmujemy od drugiego równania pierwsze (żeby skrócić 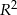 ) i mamy
) i mamy
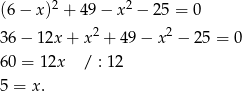
Stąd
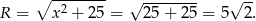
Odpowiedź: