/Szkoła średnia/Ciągi/Geometryczny/Czterowyrazowy

Zadanie nr 1988306

Różnica między drugim wyrazem ciągu geometrycznego a pierwszym wyrazem tego ciągu wynosi -6, a różnica między czwartym a pierwszym wyrazem tego ciągu jest równa -18. Oblicz trzeci wyraz tego ciągu.

Wersja PDF

Rozwiązanie

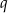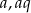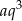Jeżeli oznaczymy pierwszy wyraz ciągu przez a , a iloraz przez q to pierwszy, drugi i czwarty wyraz danego ciągu to a,aq i aq3 odpowiednio. Mamy zatem

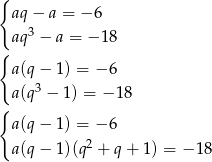
{ aq − a = − 6 3 { aq − a = − 18 a(q − 1) = − 6 a(q3 − 1) = − 18 { a(q − 1) = − 6 a(q − 1)(q2 + q + 1) = − 18

Podstawiając w drugim równaniu z pierwszego mamy

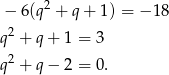
− 6(q2 + q + 1) = − 18 2 q + q + 1 = 3 q2 + q − 2 = 0 .

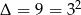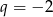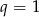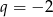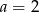Liczymy dalej Δ = 9 = 32 , q = − 2 lub q = 1 . Drugie z tych rozwiązań nie spełnia powyższego układu równań, zatem q = − 2 i a = 2 . Zatem trzeci wyraz to 2 aq = 8 .  
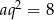Odpowiedź: 8

Wersja PDF