Zadanie nr 2306341
Liczby  i
i 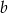 są pierwiastkami równania
są pierwiastkami równania 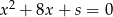 , a liczby
, a liczby  i
i 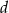 są pierwiastkami równania
są pierwiastkami równania 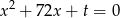 . Ciąg
. Ciąg 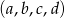 jest malejącym ciągiem geometrycznym. Oblicz
jest malejącym ciągiem geometrycznym. Oblicz  i
i 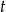 .
.
Rozwiązanie
Skoro liczby 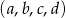 tworzą malejący ciąg geometryczny, to muszą być postaci
tworzą malejący ciąg geometryczny, to muszą być postaci 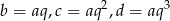 , gdzie
, gdzie 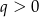 (ciąg będzie malejący, gdy
(ciąg będzie malejący, gdy 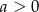 i
i 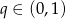 lub gdy
lub gdy 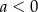 i
i 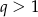 ). Zapiszmy teraz wzory Viète’a.
). Zapiszmy teraz wzory Viète’a.
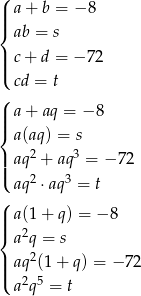
Dzielimy teraz stronami trzecie równanie przez pierwsze i mamy
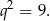
Jak zauważyliśmy, 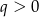 , więc
, więc 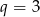 . Wtedy z pierwszego równania
. Wtedy z pierwszego równania
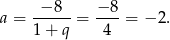
Teraz z równań drugiego i czwartego mamy
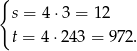
Odpowiedź: