/Szkoła średnia/Ciągi/Geometryczny/Czterowyrazowy

Zadanie nr 2311902

Dodaj do ulubionych
Dodaj do rozwiązanych

Dany jest czterowyrazowy ciąg 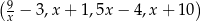(9 ) x − 3,x + 1,5x − 4 ,x+ 10 . Oblicz wszystkie wartości x , dla których ten ciąg jest geometryczny.

Rozwiązanie

Podane cztery wyrazy tworzą ciąg geometryczny, więc kwadrat trzeciego wyrazu jest iloczynem dwóch sąsiednich (na razie nie patrzymy na pierwszy wyraz, bo jest najbardziej skomplikowany). Zatem

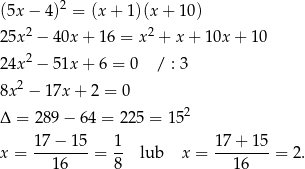
(5x − 4)2 = (x + 1 )(x+ 10) 2 2 25x − 40x + 16 = x + x + 10x + 1 0 24x2 − 51x + 6 = 0 / : 3 2 8x − 17x + 2 = 0 Δ = 289 − 64 = 2 25 = 152 17−--15- 1- 17+--15- x = 16 = 8 lub x = 16 = 2.

Dla tych wartości x otrzymujemy odpowiednio ciągi

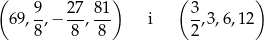
( ) ( ) 69, 9,− 27-, 81 i 3,3 ,6 ,12 8 8 8 2

Tylko drugi z tych ciągów jest geometryczny (z ilorazem 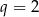q = 2 ).  
Odpowiedź: x = 2

Wersja PDF