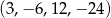/Szkoła średnia/Ciągi/Geometryczny/Czterowyrazowy

Zadanie nr 4391715

Liczby 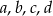a,b,c,d są czterema kolejnymi wyrazami ciągu geometrycznego. Trzecia liczba jest o 9 większa od pierwszej, a druga liczba jest o 18 większa od czwartej. Wyznacz te liczby.

Wersja PDF

Rozwiązanie

Jeżeli oznaczymy te liczby przez 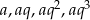2 3 a,aq,aq ,aq to mamy układ równań

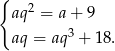
{ 2 aq = a + 9 aq = aq3 + 18.

Jeżeli odejmiemy od drugiego równania dwa razy pierwsze (żeby skrócić 18 i 9), to dostaniemy równanie, w którym skróci się a . Liczymy

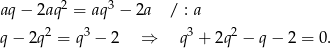
2 3 aq − 2aq = aq − 2a / : a q − 2q2 = q3 − 2 ⇒ q3 + 2q2 − q− 2 = 0.

Można standardowo sprawdzać dzielniki wyrazu wolnego, ale w tym przykładzie rozkłada narzuca się sam.

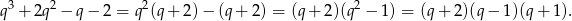
3 2 2 2 q + 2q − q − 2 = q (q + 2)− (q+ 2) = (q + 2)(q − 1) = (q + 2)(q− 1)(q+ 1).

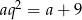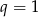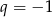Patrząc ponownie na równanie aq2 = a + 9 widać, że q = 1 i q = − 1 odpada. Zatem 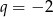q = − 2 i mamy

4a = a + 9 ⇒ a = 3.

Daje to nam ciąg 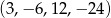(3,− 6,12 ,−2 4) .  
Odpowiedź: (3,− 6,12,− 24 )

Wersja PDF