/Szkoła średnia/Ciągi/Geometryczny/Czterowyrazowy

Zadanie nr 8544177

Dodaj do ulubionych
Dodaj do rozwiązanych

Podstawy czterech logarytmów liczby x tworzą ciąg geometryczny o ilorazie x . Wyznacz pierwszy z tych logarytmów jeśli jest on mniejszy od -1 oraz suma dwóch pierwszych logarytmów jest równa sumie dwóch pozostałych

Rozwiązanie

Oznaczmy przez 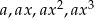2 3 a,ax,ax ,ax podstawy kolejnych logarytmów oraz niech

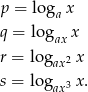
p = loga x q = logax x r = logax2 x s = logax3 x.

Ze wzoru na zmianę podstawy logarytmu mamy

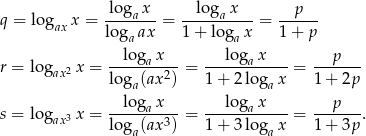
-logax- --lo-gax--- --p--- q = logax x = log ax = 1+ lo g x = 1 + p a a r = log x = --lo-gax---= ---lo-gax----= --p---- ax2 loga(ax2) 1 + 2loga x 1+ 2p lo g x lo g x s = log 3 x = -----a----= ------a-----= --p---. ax loga(ax3) 1 + 3loga x 1+ 3p

Teraz korzystamy z informacji o tym, że suma dwóch pierwszych logarytmów jest równa sumie dwóch pozostałych.

p + --p---= ---p--- + ---p--- 1+ p 1 + 2p 1 + 3p

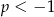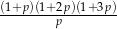Wiemy, że p < − 1 , więc możemy pomnożyć powyższą równość stronami przez (1+p-)(1+2p)(1+3p) p .

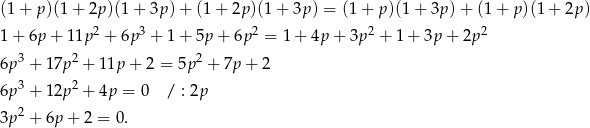
(1+ p)(1 + 2p)(1 + 3p )+ (1+ 2p)(1 + 3p) = (1 + p )(1+ 3p) + (1+ p)(1 + 2p ) 1+ 6p + 11p 2 + 6p 3 + 1+ 5p+ 6p2 = 1 + 4p + 3p2 + 1+ 3p + 2p 2 3 2 2 6p + 17p + 1 1p+ 2 = 5p + 7p + 2 6p3 + 12p 2 + 4p = 0 / : 2p 3p2 + 6p + 2 = 0.

Rozwiązujemy otrzymane równanie kwadratowe.

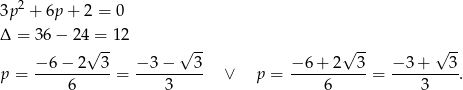
3p 2 + 6p+ 2 = 0 Δ = 36 − 24 = 12 √ -- √ -- √ -- √ -- p = −-6-−-2--3-= −-3−----3- ∨ p = −-6+--2--3-= −-3+----3. 6 3 6 3

Tylko pierwszy z tych pierwiastków jest mniejszy od -1, zatem 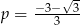√- p = −-3−--3- 3  
Odpowiedź: −-3−√-3 3

Wersja PDF