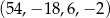/Szkoła średnia/Ciągi/Geometryczny/Czterowyrazowy

Zadanie nr 8930319

Cztery liczby tworzą ciąg geometryczny, przy czym suma pierwszej i czwartej jest równa 52, a iloczyn drugiej i trzeciej jest równy 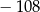− 108 . Wyznacz te liczby.

Wersja PDF

Rozwiązanie

Oznaczmy szukane liczby przez 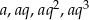2 3 a,aq,aq ,aq . Mamy zatem układ równań

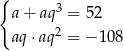
{ a+ aq3 = 52 aq ⋅aq2 = − 108

Podstawiamy 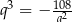3 108- q = − a2 z drugiego równania do pierwszego.

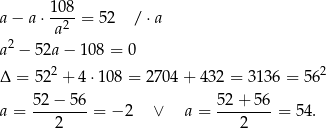
10 8 a − a ⋅--2- = 52 / ⋅a a a 2 − 52a − 1 08 = 0 2 2 Δ = 52 + 4 ⋅108 = 2704 + 432 = 3136 = 56 52-−-56- 52-+-5-6 a = 2 = − 2 ∨ a = 2 = 54.

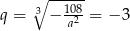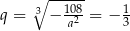Mamy wtedy odpowiednio ∘ ----- q = 3 − 1028= − 3 a i ∘ ----- q = 3 − 1082-= − 1 a 3 . Są więc dwa ciągi spełniające warunki zadania:

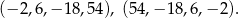
(− 2,6 ,−1 8,54), (5 4,− 18,6,− 2).

 
Odpowiedź: 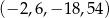(− 2,6,− 18,54 ) lub (54,− 18 ,6 ,−2 )

Wersja PDF