/Szkoła średnia/Ciągi/Geometryczny/Czterowyrazowy

Zadanie nr 9438809

Cztery liczby tworzą ciąg geometryczny. Wyznacz te liczby wiedząc, że suma pierwszej i czwartej wynosi 36, a suma drugiej i trzeciej liczby wynosi 24.

Wersja PDF

Rozwiązanie

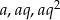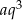Oznaczmy podane liczby przez 2 a,aq,aq i 3 aq . Mamy zatem dwa równania

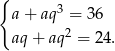
{ a+ aq3 = 36 aq+ aq2 = 24.

Jeżeli podzielimy pierwsze równanie przez drugie (żeby skrócić a ) to mamy

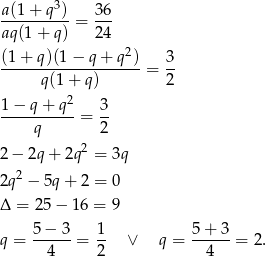
3 a(1-+-q-)-= 36- aq(1 + q) 24 2 (1-+-q)(1-−-q+--q-) = 3- q(1 + q ) 2 1 − q+ q2 3 ---------- = -- q 2 2− 2q+ 2q2 = 3q 2 2q − 5q+ 2 = 0 Δ = 25− 16 = 9 q = 5-−-3-= 1- ∨ q = 5-+-3-= 2 . 4 2 4

Z pierwszego równania mamy wtedy odpowiednio

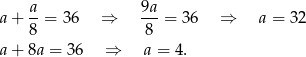
a + a-= 36 ⇒ 9a-= 36 ⇒ a = 32 8 8 a + 8a = 36 ⇒ a = 4.

Daje to nam dwa ciągi

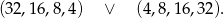
(3 2,16,8,4) ∨ (4,8,1 6,32).

 
Odpowiedź: 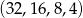(32,16 ,8,4) lub (4 ,8 ,16,32)

Wersja PDF