Zadanie nr 9717786
Liczby 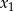 i
i 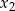 są pierwiastkami równania
są pierwiastkami równania 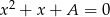 , a liczby
, a liczby 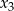 i
i 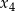 są pierwiastkami równania
są pierwiastkami równania 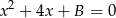 . Wiadomo, że ciąg
. Wiadomo, że ciąg 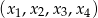 jest ciągiem geometrycznym o wyrazach całkowitych. Wyznacz
jest ciągiem geometrycznym o wyrazach całkowitych. Wyznacz 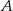 i
i 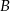 .
.
Rozwiązanie
Ponieważ liczby 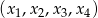 tworzą ciąg geometryczny to są one postaci
tworzą ciąg geometryczny to są one postaci
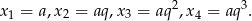
dla pewnych  i
i 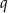 . Wzory Viète’a dają nam równania
. Wzory Viète’a dają nam równania
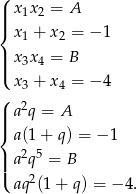
Podstawiając w ostatnim równaniu za 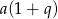 z drugiego równania, otrzymujemy
z drugiego równania, otrzymujemy
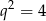
Zatem 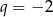 lub
lub 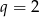 . Z drugiego równania mamy wtedy
. Z drugiego równania mamy wtedy 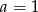 lub
lub 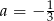 . Ponieważ ciąg ma mieć wyrazy całkowite, to drugie rozwiązanie odrzucamy. Z pierwszego i trzeciego równania otrzymujemy wtedy
. Ponieważ ciąg ma mieć wyrazy całkowite, to drugie rozwiązanie odrzucamy. Z pierwszego i trzeciego równania otrzymujemy wtedy 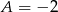 i
i 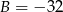 .
.
Na koniec wypada sprawdzić, że otrzymane równania
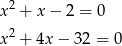
mają rzeczywiście pierwiastki, ale to jest łatwe (liczmy 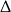 -ę).
-ę).
Odpowiedź: