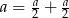Zadanie nr 5129110
Liczbę dodatnią 
przedstaw w postaci sumy dwóch takich składników, aby suma ich sześcianów była najmniejsza.
Rozwiązanie
Jeżeli oznaczymy jeden ze składników przez 
to drugi jest równy 
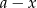. Zatem suma ich sześcianów jest równa
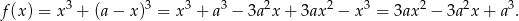
Wykresem tej funkcji jest parabola o ramionach skierowanych do góry (bo 
jest dodatnie!) oraz wierzchołku w punkcie
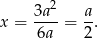
Zatem minimalną sumę sześcianów otrzymamy dla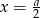 
.
Odpowiedź: 
