/Szkoła średnia/Zadania z treścią/Zarobki

Zadanie nr 1901016

Dodaj do ulubionych
Dodaj do rozwiązanych

Przystań jachtowa dysponuje 80 miejscami w hangarze. Opłata za zimowanie jednego jachtu wynosi 470 zł. Przystań udziela specjalnej zniżki firmom zimującym więcej niż 44 jachty. Wówczas opłata za każdy jacht zimowany przez firmę jest niższa o 5 zł pomnożone przez liczbę jachtów powyżej 44. Przy jakiej liczbie zimowanych jachtów przez jedną firmę (powyżej 44) przystań osiąga maksymalny możliwy przychód?

Rozwiązanie

Oznaczmy przez x liczbę jachtów. Zastanówmy się ile musimy zapłacić za jeden jacht jeżeli zimujemy x jachtów (x > 44 ):

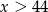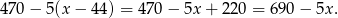
470 − 5(x − 44 ) = 470 − 5x + 220 = 690 − 5x.

Zatem cenę jaką musi zapłacić firma za zimowanie x jachtów możemy zapisać jako funkcję

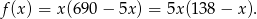
f (x) = x(69 0− 5x) = 5x (138− x).

Jest to trójmian kwadratowy o ujemnym współczynniku przy najwyższej potędze. Zatem wykres jest parabolą zwróconą ramionami w dół. Funkcja 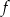f przyjmuje więc największą wartość w wierzchołku, czyli dokładnie w środku między pierwiastkami. Maksymalny przychód otrzymamy więc dla

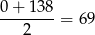
0+-1-38- 2 = 69

jachtów.  
Odpowiedź: 69

Wersja PDF