/Szkoła średnia/Zadania z treścią/Zarobki

Zadanie nr 9309121

Dodaj do ulubionych
Dodaj do rozwiązanych

Mariusz Czerkawski i Jimmy O’Brien w jednym sezonie NHL zdobyli w sumie 100 bramek. Kluby obu zawodników za każdą zdobytą bramkę wypłacały hokeistom z góry ustaloną premię. Po sezonie okazało się, że obaj zawodnicy otrzymali za strzelone bramki równe kwoty. Gdyby Czerkawski zdobył tyle bramek ile O’Brien, to otrzymałby 72000$, zaś gdyby drugi strzelił tyle bramek ile pierwszy, to otrzymałby 32000$. Oblicz, ile bramek zdobył każdy z nich i jaka była wysokość premii w obu klubach za strzelenie bramki.

Rozwiązanie

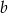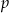Jeżeli przez b i p oznaczymy ilość bramek i wysokość premii Czerkawskiego, to na podstawie podanych informacji możemy wyznaczyć te liczby dla O’Brien’a. Mianowicie strzelił on 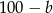100 − b bramek i miał premię w wysokości 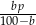--bp- 100−b za jedną bramkę. Pozostałe dwie informacje dają nam układ równań

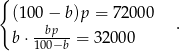
{ (100− b)p = 7 2000 . b⋅ -bp--= 32000 100−b

Podstawmy w drugim równaniu 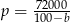-72000 p = 100−b ,

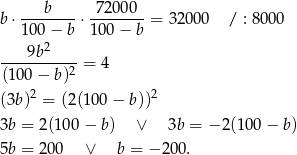
b 72000 b⋅ --------⋅--------= 32000 / : 8000 100−2 b 100 − b ---9b------= 4 (100 − b)2 2 2 (3b) = (2(100 − b)) 3b = 2(100 − b) ∨ 3b = − 2(100 − b) 5b = 200 ∨ b = − 200.

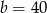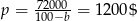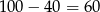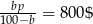Oczywiście drugie rozwiązanie odrzucamy i dostajemy b = 40 . Stąd p = 7120000−0b = 12 00$ . Odpowiednie liczby dla O’Brien’a to 100 − 40 = 60 i --bp- 100−b = 800$ .  
Odpowiedź: Czerkawski: 40, 1200$, O’Brien 60, 800$

Wersja PDF