/Szkoła średnia/Równania/Kwadratowe/Z parametrem/Różne

Zadanie nr 2437644

Wyznacz tę wartość parametru 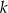k , dla której suma kwadratów dwóch różnych pierwiastków równania 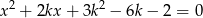x2 + 2kx + 3k2 − 6k − 2 = 0 jest największa z możliwych.

Wersja PDF

Rozwiązanie

Na początku sprawdźmy kiedy równanie ma dwa pierwiastki.

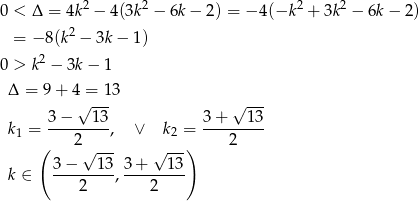
2 2 2 2 0 < Δ = 4k − 4(3k − 6k − 2 ) = − 4(−k + 3k − 6k− 2) = −8 (k2 − 3k − 1 ) 2 0 > k − 3k − 1 Δ = 9 + 4 = 1 3 √ --- √ --- 3−----13- 3-+---13- k 1 = 2 , ∨ k2 = 2 ( √ --- √ ---) k ∈ 3-−---1-3, 3-+--13- 2 2

Na mocy wzorów Viete’a mamy

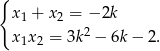
{ x + x = − 2k 1 2 2 x1x2 = 3k − 6k − 2.

Zatem

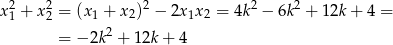
x21 + x22 = (x 1 + x 2)2 − 2x 1x2 = 4k2 − 6k2 + 12k + 4 = 2 = − 2k + 12k + 4

Wykresem tego wyrażenia jest parabola o ramionach skierowanych w dół, a jego dziedziną zbiór 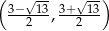( √ -- √ --) 3−--13, 3+-13 2 2 . Ponieważ pierwsza współrzędna wierzchołka tej paraboli 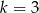k = 3 znajduje się w tym przedziale, to właśnie w nim powyższe wyrażenie przyjmuje największą wartość.  
Odpowiedź: k = 3

Wersja PDF