Zadanie nr 3514260
Liczby 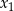 i
i 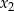 są wszystkimi pierwiastkami rzeczywistymi równania
są wszystkimi pierwiastkami rzeczywistymi równania 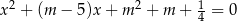 , przy czym zakładamy, że
, przy czym zakładamy, że 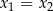 w przypadku, gdy równanie ma tylko jedno rozwiązanie. Zbadaj, dla jakich wartości parametru
w przypadku, gdy równanie ma tylko jedno rozwiązanie. Zbadaj, dla jakich wartości parametru 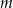 , wyrażenie
, wyrażenie 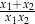 przyjmuje wartość najmniejszą. Oblicz tę wartość.
przyjmuje wartość najmniejszą. Oblicz tę wartość.
Rozwiązanie
Na początku sprawdzamy kiedy dane równanie ma pierwiastki rzeczywiste.
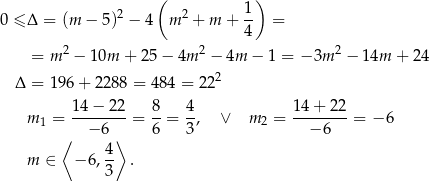
Powyższy rachunek mogliśmy trochę uprościć zauważając, że
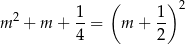
i
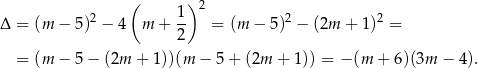
Tak czy inaczej, na mocy wzorów Viete’a mamy
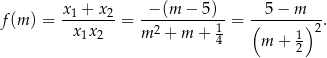
Ze względu na mianownik musimy dodatkowo założyć, że 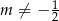 . Liczymy pochodną tej funkcji
. Liczymy pochodną tej funkcji
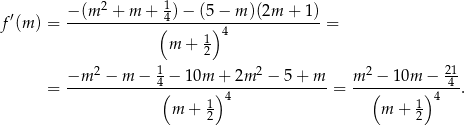
Rozkładamy jeszcze trójmian w liczniku.
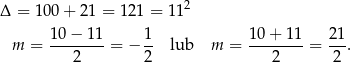
Mamy zatem
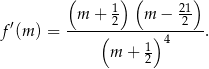
To oznacza, że pochodna jest dodatnia na przedziale 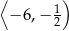 i ujemna na przedziale
i ujemna na przedziale 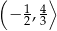 . Zatem funkcja
. Zatem funkcja 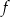 rośnie w przedziale
rośnie w przedziale 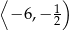 i maleje w przedziale
i maleje w przedziale 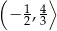 . To z kolei oznacza, że najmniejsza wartość funkcji
. To z kolei oznacza, że najmniejsza wartość funkcji 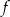 to albo
to albo 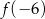 albo
albo 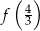 . Liczymy każdą z tych wartości
. Liczymy każdą z tych wartości
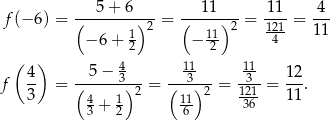
Najmniejszą wartością funkcji 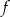 jest więc
jest więc 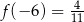 .
.
Odpowiedź: 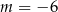 , najmniejsza wartość:
, najmniejsza wartość: