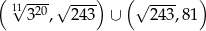Zadanie nr 5836204

Liczba 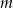jest sumą odwrotności dwóch różnych pierwiastków równania

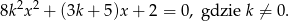
2 2 8k x + (3k + 5 )x+ 2 = 0, gdzie k ⁄= 0.

Wyznacz zbiór wartości funkcji określonej wzorem 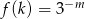f(k ) = 3−m .

Rozwiązanie

Sprawdźmy najpierw, kiedy równanie ma dwa różne pierwiastki.

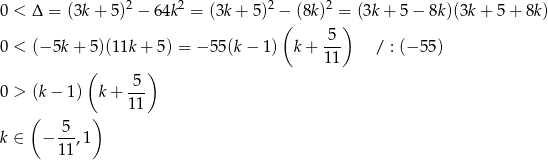
2 2 2 2 0 < Δ = (3k + 5) − 64k = (3k + 5) −( (8k) =)(3k + 5− 8k )(3k+ 5+ 8k) -5- 0 < (− 5k + 5)(11k + 5) = − 55(k− 1) k+ 11 / : (− 55) ( ) 0 > (k − 1) k + -5- 1 1 ( 5 ) k ∈ − --,1 11

(Pamiętamy, że jednocześnie obowiązuje założenie 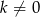k ⁄= 0 .) Przy tym założeniu możemy zapisać wzory Viète’a

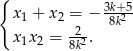
{ 3k+5 x1 + x 2 = − 8k2 x1x2 = 82k2.

Mamy stąd

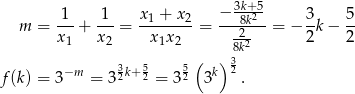
1 1 x + x − 3k+25 3 5 m = ---+ ---= -1----2-= --82k---= − --k− -- x 1 x2 x1x 2 8k2 2 2 3 5 5( )3 f(k) = 3−m = 3 2k+2 = 3 2 3k 2 .

Otrzymana funkcja jest oczywiście rosnąca (bo rosnąca jest funkcja 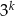k 3 ), więc jej zbiorem wartości jest

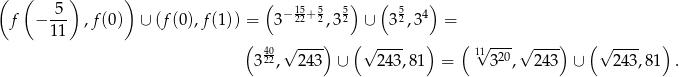
( ( ) ) ( ) ( ) f − -5- ,f(0) ∪ (f (0),f(1)) = 3−1252+ 52,352 ∪ 3 52,34 = 11 ( 40 √ ---) ( √ ---- ) ( 1√1--- √ ----) (√ ---- ) 322, 243 ∪ 243,81 = 320, 243 ∪ 243,8 1 .

Odpowiedź: ( 11√ --- √ ---) (√ ---- ) 320, 243 ∪ 2 43,81