/Szkoła średnia/Równania/Kwadratowe/Z parametrem/Różne

Zadanie nr 7684596

Dodaj do ulubionych
Dodaj do rozwiązanych

Dla jakich wartości parametru 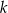k suma kwadratów pierwiastków równania 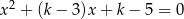x 2 + (k − 3)x + k − 5 = 0 jest najmniejsza?

Rozwiązanie

Na początku sprawdźmy kiedy równanie ma pierwiastki.

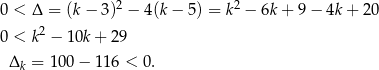
2 2 0 < Δ = (k− 3) − 4(k− 5) = k − 6k+ 9− 4k+ 20 0 < k2 − 10k + 29 Δk = 100 − 116 < 0.

To oznacza, że równanie ma zawsze dwa różne pierwiastki rzeczywiste.

Na mocy wzorów Viete’a mamy

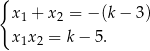
{ x1 + x2 = − (k − 3) x x = k− 5 . 1 2

Zatem

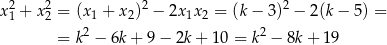
2 2 2 2 x 1 + x 2 = (x1 + x2) − 2x1x2 = (k − 3) − 2(k − 5) = = k2 − 6k + 9− 2k + 1 0 = k2 − 8k+ 19

Wykresem tego wyrażenia jest parabola o ramionach skierowanych w górę, więc najmniejszą wartość otrzymamy w wierzchołku tej paraboli, czyli dla

8 k = --= 4. 2

 
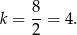
Odpowiedź: k = 4

Wersja PDF