Zadanie nr 7074539

W amﬁteatrze jest 20 rzędów ponumerowanych krzeseł. W pierwszym rzędzie jest 37 krzeseł, a w każdym następnym rzędzie są o trzy miejsca więcej niż w poprzednim. Miejsca w pierwszym rzędzie mają numery od 1 do 37, w drugim od 38 do 77 itd.

Jakie numery mają miejsca w ostatnim rzędzie?
W amﬁteatrze odbędzie się koncert Kasi Kowalskiej. Ela kupiła na ten koncert bilet z numerem miejsca 666. W którym rzędzie będzie siedziała Ela?

Rozwiązanie

Policzmy ile jest krzeseł w pierwszych 19 rzędach. Jest ich
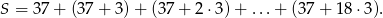
$S = 37 + (37 + 3) + (37 + 2 ⋅3)+ ...+ (37 + 18 ⋅3).$

Wyrażenie to to suma 19 początkowych wyrazów ciągu arytmetycznego o pierwszym wyrazie 37 i różnicy 3. Ze wzoru na sumę początkowych wyrazów ciągu arytmetycznego mamy

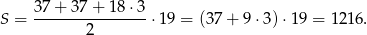
$S = 37-+-37-+-18-⋅3-⋅19 = (37+ 9⋅3 )⋅19 = 1216. 2$

Tak więc w 20 rzędzie numery miejsc zaczynają się od 1217. Ponadto w tym rzędzie są

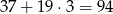
$37+ 19 ⋅3 = 94$

miejsca.
Odpowiedź: od 1217 do 1310
Na mocy poprzedniego podpunktu w pierwszych rzędach jest
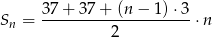
$S = 37-+-37-+-(n-−-1)-⋅3-⋅n n 2$

miejsc. Musimy zatem sprawdzić dla jakiego największego

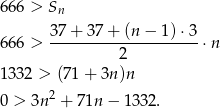
$6 66 > Sn 6 66 > 37-+-3-7+-(n-−--1)⋅3-⋅n 2 1 332 > (71 + 3n )n 0 > 3n2 + 71n − 1 332.$

Liczymy, ,

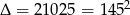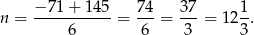
$n = −-71-+-145-= 74-= 37-= 121. 6 6 3 3$

Widać zatem, że 12 rząd to ostatni, w którym numery miejsc są mniejsze niż 666. Tak więc miejsce o numerze 666 jest w 13 rzędzie.
Odpowiedź: W 13 rzędzie.