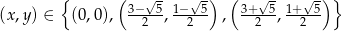/Szkoła średnia/Zadania z treścią/Własności liczb/Różne

Zadanie nr 2042576

Suma dwóch liczb, ich iloczyn i różnica ich kwadratów są równe. Wyznacz te liczby.

Wersja PDF

Rozwiązanie

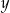Jeżeli oznaczymy szukanie liczby przez x i y , to mamy układ równań

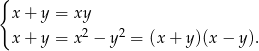
{ x + y = xy x + y = x 2 − y 2 = (x+ y)(x − y).

Chcielibyśmy podzielić drugie równanie przez 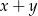x + y , ale zanim to zrobimy musimy najpierw ustalić co się dzieje dla 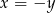x = −y . Drugie równanie jest oczywiście spełnione, a pierwsze przyjmuje postać

xy = 0.

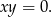
Stąd otrzymujemy jedno rozwiązanie układu: 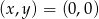(x,y) = (0,0) .

Załóżmy teraz, że 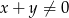x + y ⁄= 0 , wtedy drugie równanie przyjmuje postać

1 = x − y.

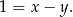
Podstawiamy teraz 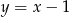y = x − 1 do pierwszego równania.

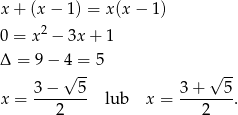
x+ (x− 1) = x(x − 1 ) 0 = x2 − 3x + 1 Δ = 9 − 4 = 5 √ -- √ -- 3-−---5- 3-+---5- x = 2 lub x = 2 .

Mamy wtedy

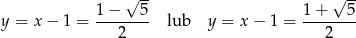
√ -- √ -- 1− 5 1+ 5 y = x − 1 = -------- lub y = x − 1 = -------- 2 2

odpowiednio.  
Odpowiedź: { ( √- √ -) ( √ - √ -)} (x,y) ∈ (0,0), 3−25-, 1−2-5 , 3+2-5, 1+2-5

Wersja PDF