/Szkoła średnia/Zadania z treścią/Własności liczb/Różne

Zadanie nr 2087986

Suma stu kolejnych liczb naturalnych, które przy dzieleniu przez 5 dają resztę 2 wynosi 30950. Wyznacz najmniejszą i największą z tych liczb.

Wersja PDF

Rozwiązanie

Liczby, o których mowa w zadaniu, tworzą ciąg arytmetyczny o różnicy 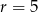r = 5 i pierwszym wyrazie postaci 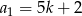a1 = 5k + 2 . Ostatni wyraz tego ciągu jest równy

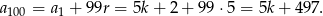
a100 = a1 + 99r = 5k + 2 + 99 ⋅5 = 5k + 497 .

Ze wzoru na sumę ciągu arytmetycznego mamy równanie

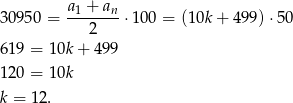
3095 0 = a1-+-an-⋅100 = (10k+ 499) ⋅50 2 619 = 10k+ 499 120 = 10k k = 12.

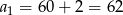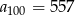Zatem a = 60 + 2 = 62 1 i a = 557 100 .  
Odpowiedź: 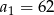a1 = 6 2 i a100 = 557

Wersja PDF