/Szkoła średnia/Zadania z treścią/Własności liczb/Różne

Zadanie nr 2094242

Dodaj do ulubionych
Dodaj do rozwiązanych

Różnica dwóch liczb naturalnych dodatnich mniejszych od 160 jest równa 119, a ich największy wspólny dzielnik jest równy 17. Wyznacz te liczby.

Rozwiązanie

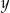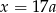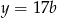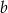Oznaczmy szukane liczby przez x i y . Skoro największy wspólny dzielnik tych liczb jest równy 17, to są one postaci x = 17a i y = 17b dla pewnych względnie pierwszych liczb a i b . Mamy zatem

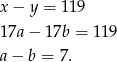
x − y = 11 9 17a − 17b = 119 a− b = 7.

Zauważmy ponadto, że z założenia

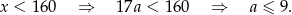
x < 16 0 ⇒ 17a < 1 60 ⇒ a ≤ 9.

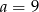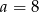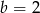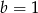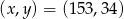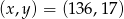W takim razie a = 9 lub a = 8 . Mamy wtedy odpowiednio b = 2 i b = 1 . Daje to nam dwa rozwiązania: (x,y) = (153 ,34) lub (x ,y) = (136,17 ) .  
Odpowiedź: 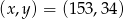(x,y ) = (153,34) lub (x,y ) = (136,17)

Wersja PDF