/Szkoła średnia/Zadania z treścią/Własności liczb/Różne

Zadanie nr 3694401

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz cztery kolejne liczby całkowite takie, że największa z nich jest równa sumie kwadratów trzech pozostałych liczb.

Rozwiązanie

Sposób I

Oznaczmy szukane przez 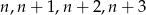n ,n + 1,n + 2,n + 3 . Musimy zatem wyznaczyć całkowite rozwiązania równania

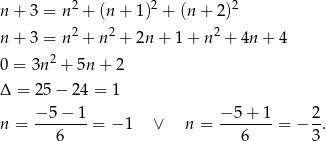
2 2 2 n+ 3 = n + (n + 1) + (n + 2) n+ 3 = n2 + n 2 + 2n + 1+ n2 + 4n + 4 0 = 3n 2 + 5n + 2 Δ = 2 5− 24 = 1 n = −-5-−-1 = − 1 ∨ n = −-5+--1 = − 2-. 6 6 3

Ponieważ n ma być liczbą całkowitą jedynymi liczbami spełniającymi warunki zadania są − 1 ,0,1,2 .

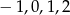Sposób II

Oznaczmy szukane liczby przez 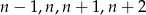n − 1,n ,n + 1,n+ 2 . Musimy zatem wyznaczyć całkowite rozwiązania równania

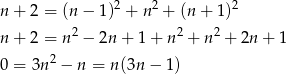
n + 2 = (n − 1)2 + n2 + (n + 1)2 2 2 2 n + 2 = n − 2n + 1 + n + n + 2n + 1 0 = 3n2 − n = n (3n − 1)

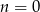Ponieważ n ma być liczbą całkowitą, musi być n = 0 i szukane liczby to − 1,0,1,2 .  
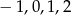Odpowiedź: − 1,0,1,2

Wersja PDF