/Szkoła średnia/Funkcje/Logarytm/Różne

Zadanie nr 5924602

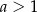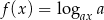Niech a > 1 będzie ustaloną liczbą rzeczywistą i f(x) = logax a .

  • Wyznacz dziedzinę funkcji f .
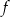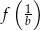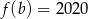  • Oblicz ( ) f 1 b jeżeli f (b) = 2020 .
Wersja PDF

Rozwiązanie

  • Wzór definiujący funkcję 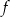f ma sens pod warunkiem, że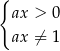
    { ax > 0 ax ⁄= 1

    Tak jest jeżeli

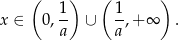
    ( 1 ) ( 1 ) x ∈ 0,-- ∪ -,+ ∞ . a a

     
    Odpowiedź: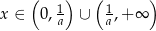 ( ) ( ) x ∈ 0, 1a ∪ 1a,+ ∞

  • Wiemy, że (korzystamy ze wzoru na zmianę podstawy logarytmu)
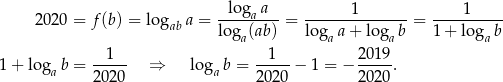
    log a 1 1 2020 = f(b) = logab a = ----a----= -------------- = ---------- loga(ab) logaa + loga b 1+ loga b --1-- --1-- 201-9 1+ lo gab = 2020 ⇒ loga b = 202 0 − 1 = − 202 0.

    Stąd

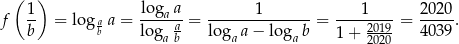
    ( ) f 1- = loga a = loga-a = ------1------- = ----1--- = 2020-. b b loga ab lo gaa − loga b 1 + 22001290 4039

     
    Odpowiedź: 2020 4039

Wersja PDF