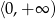/Szkoła średnia/Funkcje - wykresy/Z pierwiastkami/Z kwadratową

Zadanie nr 3176792

Dodaj do ulubionych
Dodaj do rozwiązanych

Naszkicuj wykres funkcji: 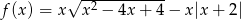√ -2---------- f(x) = x x − 4x + 4 − x|x + 2| . Wyznacz wartość największą tej funkcji oraz jej maksymalne przedziały monotoniczności.

Rozwiązanie

Przekształćmy wzór funkcji.

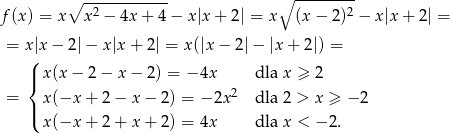
∘ ------------ ∘ --------- f (x ) = x x2 − 4x+ 4− x|x+ 2| = x (x − 2 )2 − x |x + 2| = = x(|x − 2 |− x|x + 2| = x(|x − 2|− |x+ 2|) = | x(x − 2 − x − 2) = − 4x dla x ≥ 2 { 2 = | x(−x + 2 − x − 2) = − 2x dla 2 > x ≥ − 2 ( x(−x + 2 + x + 2) = 4x dla x < − 2.

Teraz bez trudu szkicujemy wykres.

PIC

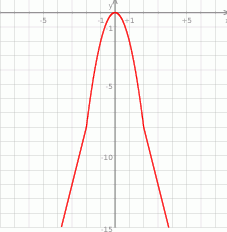
Z wykresu widzimy, że wartość największa to 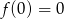f (0) = 0 . Ponadto funkcja rośnie w przedziale 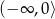(− ∞ ,0⟩ i maleje w przedziale ⟨0,+ ∞ ) .  
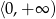Odpowiedź: 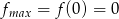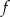fmax = f(0) = 0 , f rośnie w 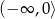(− ∞ ,0⟩ i maleje w ⟨0,+ ∞ )

Wersja PDF