Zadanie nr 3424936
Naszkicuj wykres funkcji 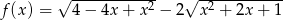 . Korzystając z wykresu funkcji
. Korzystając z wykresu funkcji 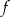 określ liczbę rozwiązań równania
określ liczbę rozwiązań równania 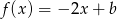 w zależności od wartości parametru
w zależności od wartości parametru 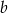 .
.
Rozwiązanie
Przekształćmy podany wzór funkcji
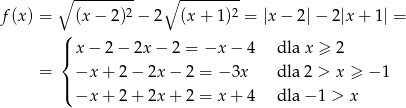
Teraz bez trudu rysujemy wykres.
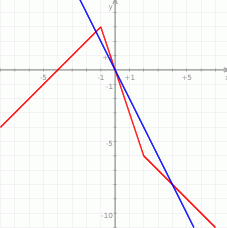
Na tym samym wykresie narysowaliśmy wykres funkcji 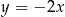 . Funkcja
. Funkcja 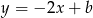 powstaje oczywiście z
powstaje oczywiście z 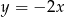 przez przesunięcie wzdłuż osi
przez przesunięcie wzdłuż osi 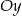 . Z narysowanych wykresów widać, że kluczowe jest znalezienie wartości
. Z narysowanych wykresów widać, że kluczowe jest znalezienie wartości 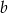 , dla których prosta
, dla których prosta 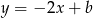 przechodzi przez „rogi” wykresu
przechodzi przez „rogi” wykresu 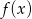 , czyli przez punkty
, czyli przez punkty 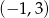 i
i 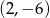 . Łatwo te wartości
. Łatwo te wartości 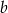 wyliczyć (wstawiając te punkty do wzoru), wynoszą one odpowiednio
wyliczyć (wstawiając te punkty do wzoru), wynoszą one odpowiednio 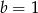 i
i 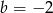 .
.
Widać teraz, że punktów wspólnych podanych funkcji jest
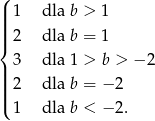
Odpowiedź: