/Szkoła średnia/Funkcje - wykresy/Z pierwiastkami/Z kwadratową

Zadanie nr 7622481

Dodaj do ulubionych
Dodaj do rozwiązanych

Naszkicuj wykres funkcji 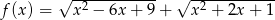√ -2---------- √ -2---------- f (x) = x − 6x + 9 + x + 2x + 1 , a następnie korzystając z otrzymanego wykresu ustal liczbę pierwiastków równania 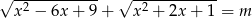√ ------------ √ ------------ x 2 − 6x + 9+ x 2 + 2x + 1 = m w zależności od parametru m , m ∈ R .

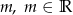Rozwiązanie

Gołym okiem widać, że mamy kwadraty pod pierwiastkami:

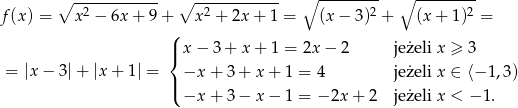
∘ ------------ ∘ ------------ ∘ --------- ∘ --------- f (x) = x 2 − 6x + 9+ x2 + 2x + 1 = (x− 3)2 + (x + 1)2 = ( |{ x − 3 + x + 1 = 2x− 2 jeżeli x ≥ 3 = |x − 3| + |x+ 1| = −x + 3 + x + 1 = 4 jeżeli x ∈ ⟨− 1,3) |( −x + 3 − x − 1 = − 2x + 2 jeżeli x < − 1.

Jeżeli ktoś nie wie w jaki sposób pozbyliśmy się wartości bezwzględnej to niech zajrzy do odpowiedniego poradnika.

Teraz bez trudu rysujemy wykres.

PIC

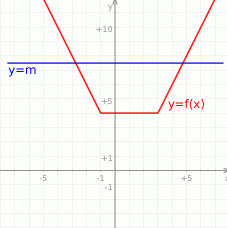
Z wykresu widzimy, że liczba rozwiązań równania 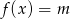f(x) = m jest równa

( |{ 0 jeżeli m < 4 |( ∞ jeżeli m = 4 2 jeżeli m > 4.
Wersja PDF