/Szkoła średnia/Funkcje - wykresy/Wielomiany/Stopnia 4

Zadanie nr 3928210

Dodaj do ulubionych
Dodaj do rozwiązanych

Dany jest wielomian 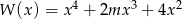4 3 2 W (x) = x + 2mx + 4x z parametrem m .

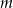  • Wiedząc, że wykres tego wielomianu jest symetryczny względem prostej 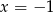x = − 1 , wyznacz m .
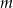  • Dla wyznaczonej wartości parametru 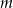m uzasadnij, że nierówność 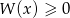W (x) ≥ 0 jest spełniona przez każdą liczbę rzeczywistą x ∈ R .

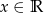Rozwiązanie

  • Jeżeli wykres ma być symetryczny względem prostej 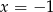x = − 1 to znaczy, że wartości funkcji 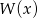W (x) w punktach położonych symetrycznie względem tej prostej muszą być równe. Np. musimy mieć 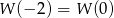W (− 2) = W (0) . To pozwoli nam wyliczyć m .
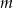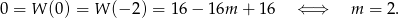
    0 = W (0) = W (− 2) = 16− 16m + 16 ⇐ ⇒ m = 2.

    Nie musimy tego robić, ale możemy jeszcze sprawdzić, że dla 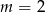m = 2 wykres rzeczywiście jest symetryczny względem prostej 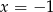x = − 1 . W tym celu zapiszmy wielomian 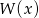W (x) w postaci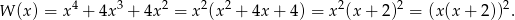

    4 3 2 2 2 2 2 2 W (x) = x + 4x + 4x = x (x + 4x + 4) = x (x+ 2) = (x(x + 2)) .

    Wykresem funkcji 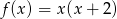f(x) = x(x+ 2) jest parabola symetryczna względem prostej 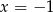x = − 1 (pionowa prosta przechodząca) przez wierzchołek, więc po podniesieniu do kwadratu nadal będziemy mieli wykres symetryczny względem tej prostej (bo nadal wartości w punktach symetrycznych względem tej prostej będą równe).  
    Odpowiedź: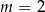 m = 2

  • Jak już zauważyliśmy w poprzednim podpunkcie, mamy
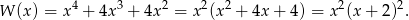
    W (x) = x 4 + 4x 3 + 4x 2 = x2(x2 + 4x + 4) = x2(x + 2)2.

    Jest jasne, że to wyrażenie jest nieujemne.

Wersja PDF