/Szkoła średnia/Funkcje - wykresy/Wielomiany/Stopnia 3

Zadanie nr 2756111

Wykres funkcji 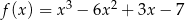3 2 f(x) = x − 6x + 3x − 7 przesunięto o wektor 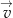→ v i wyniku tej operacji otrzymano wykres, który jest symetryczny względem początku układu współrzędnych. Wyznacz współrzędne wektora →v .

Wersja PDF

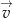Rozwiązanie

Sposób I

Jeżeli wykres funkcji 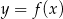y = f(x) przesunięto o wektor → v = [a,b] , to otrzymano wykres funkcji

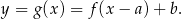
y = g(x) = f(x − a)+ b.

To, że wykres ten jest symetryczny względem początku układu współrzędnych oznacza, że dla każdej liczby 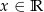x ∈ R mamy

g(−x ) = −g (x)

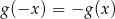
(czyli funkcja 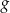g jest nieparzysta).

PIC

Pozostało więc rozwiązać równanie

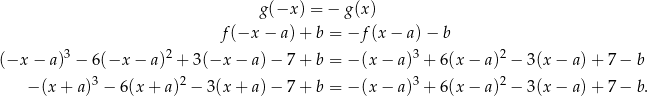
g(−x ) = − g (x) f (−x − a)+ b = −f (x − a) − b (−x − a)3 − 6(−x − a)2 + 3(−x − a)− 7+ b = − (x− a)3 + 6(x− a)2 − 3(x− a)+ 7− b 3 2 3 2 − (x+ a) − 6 (x+ a) − 3 (x+ a)− 7+ b = − (x− a) + 6(x− a) − 3(x− a)+ 7− b.

Stąd

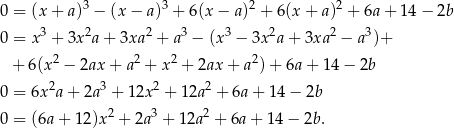
0 = (x + a)3 − (x − a)3 + 6(x − a)2 + 6(x + a)2 + 6a + 14 − 2b 3 2 2 3 3 2 2 3 0 = x + 3x a + 3xa + a − (x − 3x a+ 3xa − a )+ + 6(x2 − 2ax + a2 + x2 + 2ax + a2) + 6a + 14 − 2b 0 = 6x2a + 2a 3 + 12x 2 + 12a2 + 6a+ 14 − 2b 2 3 2 0 = (6a + 12)x + 2a + 12a + 6a + 14− 2b.

Wiemy, że równość ta ma być spełniona dla każdej wartości 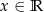x ∈ R , więc funkcja kwadratowa z prawej strony musi być stale równa zero. Stąd

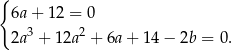
{ 6a + 1 2 = 0 2a 3 + 1 2a2 + 6a+ 14− 2b = 0.

Z pierwszego równania mamy 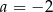a = − 2 . Wtedy z drugiego równania

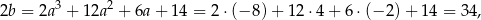
3 2 2b = 2a + 12a + 6a + 1 4 = 2⋅ (− 8)+ 1 2⋅4 + 6 ⋅(− 2)+ 14 = 34 ,

czyli 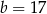b = 1 7 .

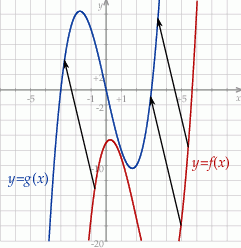
Sposób II

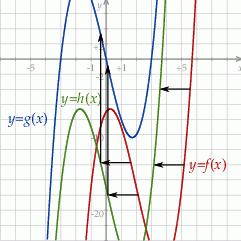
Jeżeli naszkicujemy typowy wykres wielomianu trzeciego stopnia, to powinno stać się jasne, że jeżeli jest on symetryczny względem początku układu współrzędnych, to minimum lokalne musi przechodzić na maksimum lokalne i odwrotnie. Sprawdźmy gdzie dany wielomian ma te ekstrema. Liczymy pochodną

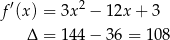
′ 2 f (x) = 3x − 12x + 3 Δ = 144− 36 = 10 8

Ponieważ 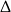Δ wygląda niezbyt atrakcyjnie, nie będziemy obliczać pierwiastków pochodnej. Zamiast tego zauważmy, że są one położone symetrycznie względem prostej

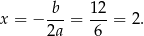
b 1 2 x = − ---= --- = 2. 2a 6

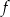Po przesunięciu muszą one leżeć symetrycznie względem osi Oy , więc widać, że wykres funkcji f musimy przesunąć o dwie jednostki 2 lewo.

PIC

Sprawdźmy z ciekawości jaką funkcję wtedy otrzymamy

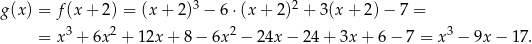
g (x) = f(x + 2) = (x+ 2)3 − 6⋅(x + 2)2 + 3(x + 2 )− 7 = 3 2 2 3 = x + 6x + 12x + 8− 6x − 24x − 24 + 3x + 6 − 7 = x − 9x− 17.

Otrzymany wykres nadal nie jest symetryczny względem początku układu współrzędnych – choćby dlatego, że 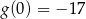g(0) = − 17 . Wykres, który jest symetryczny względem punktu 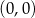(0,0) musi przez ten punkt przechodzić. W takim razie musimy jeszcze funkcję g przesunąć o 17 jednostek w górę. Otrzymamy wtedy wykres funkcji

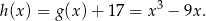
h(x) = g (x)+ 17 = x3 − 9x .

Ta funkcja jest nieparzysta, więc jej wykres jest symetryczny względem początku układu współrzędnych. Dwa przesunięcia, które wykonaliśmy łącznie dają przesunięcie o wektor

→ v = [− 2,17].

 
Odpowiedź: →v = [− 2,17]

Wersja PDF