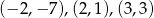/Szkoła średnia/Funkcje - wykresy/Wielomiany/Stopnia 3

Zadanie nr 3326386

Dodaj do ulubionych
Dodaj do rozwiązanych

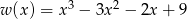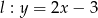Wyznacz punkty wspólne wykresu wielomianu 3 2 w (x) = x − 3x − 2x + 9 i prostej l : y = 2x − 3 .

Rozwiązanie

Musimy rozwiązać równanie 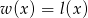w (x) = l(x ) .

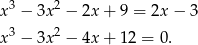
3 2 x − 3x − 2x+ 9 = 2x − 3 x 3 − 3x 2 − 4x+ 12 = 0.

Sposób I

Łatwo zauważyć, że z lewej strony możemy wyłączyć przed nawias 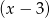(x− 3) .

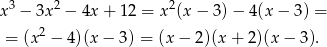
x3 − 3x2 − 4x + 12 = x 2(x− 3)− 4(x− 3) = 2 = (x − 4)(x − 3) = (x − 2)(x + 2 )(x − 3).

Odpowiadające 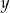y –ki wyliczamy z równania prostej

(− 2,− 7),(2,1),(3 ,3)

Sposób II

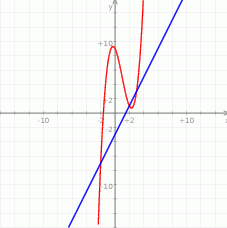
Szukamy pierwiastków całkowitych wśród dzielników wyrazu wolnego, łatwo znaleźć pierwiastek 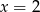x = 2 .

PIC

Dzielimy wielomian przez 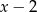x − 2 .

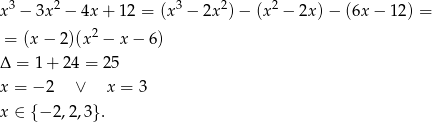
x 3 − 3x 2 − 4x+ 12 = (x3 − 2x 2)− (x 2 − 2x )− (6x− 12) = 2 = (x− 2)(x − x− 6) Δ = 1 + 24 = 25 x = − 2 ∨ x = 3 x ∈ {− 2,2,3}.

Licząc 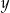y –ki mamy

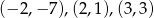
(− 2,− 7),(2,1),(3 ,3)

Na koniec obrazek.  
Odpowiedź: (− 2,− 7),(2,1),(3,3 )

Wersja PDF