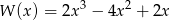Zadanie nr 4858326
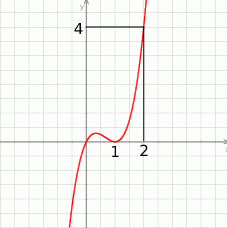
Na rysunku przedstawiony jest wykres pewnego wielomianu 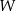 stopnia trzeciego.
stopnia trzeciego.
- Czy wielomian
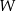 jest podzielny przez wielomian
jest podzielny przez wielomian 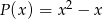 ?
? - Napisz wzór wielomianu
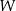 .
.
Rozwiązanie
- Z wykresu widać, że 0 i 1 są miejscami zerowymi
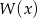 . Wielomian ten jest zatem podzielny przez
. Wielomian ten jest zatem podzielny przez 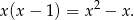
Odpowiedź: Tak - Z wykresu widać, że 0 i 1 są miejscami zerowymi
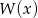 . Ponadto 1 jest pierwiastkiem podwójnym (wykres jest styczny do osi w tym punkcie). Zatem
. Ponadto 1 jest pierwiastkiem podwójnym (wykres jest styczny do osi w tym punkcie). Zatem 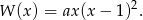
Wpółczynnik
 wyliczamy z warunku
wyliczamy z warunku 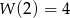 .
. 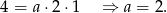
Zatem
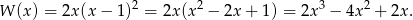
Odpowiedź: