Zadanie nr 4587533
Oblicz wartość wyrażenia 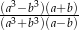 dla
dla 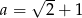 i
i 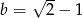 .
.
Rozwiązanie
Skorzystamy ze wzorów skróconego mnożenia
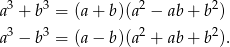
Mamy więc
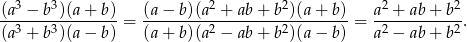
Sposób I
Podstawiamy w otrzymanym wyrażeniu podane liczby.
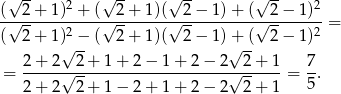
Sposób II
Zauważmy, że
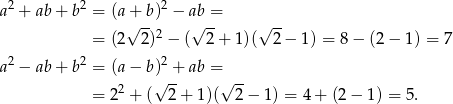
Zatem
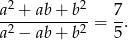
Odpowiedź: 
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Oblicz wartość wyrażenia 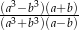 dla
dla 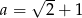 i
i 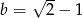 .
.
Skorzystamy ze wzorów skróconego mnożenia
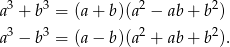
Mamy więc
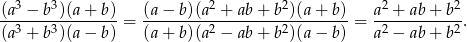
Sposób I
Podstawiamy w otrzymanym wyrażeniu podane liczby.
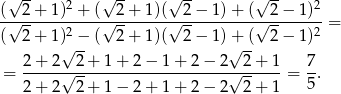
Sposób II
Zauważmy, że
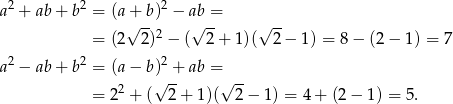
Zatem
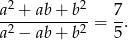
Odpowiedź: 
