/Szkoła średnia/Liczby/Potęgi i pierwiastki

Zadanie nr 5315139

Dodaj do ulubionych
Dodaj do rozwiązanych

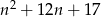Dla jakich liczb naturalnych n , liczba 2 n + 12n + 17 jest kwadratem liczby naturalnej?

Rozwiązanie

Zauważmy, że

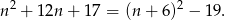
2 2 n + 12n + 17 = (n+ 6) − 19.

Sposób I

Powyższa równość oznacza, że jeżeli liczba ta jest kwadratem liczby naturalnej, to maksymalnie może to być kwadrat liczby 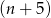(n + 5) . Z drugiej strony,

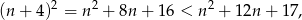
(n + 4)2 = n2 + 8n + 16 < n 2 + 1 2n + 17,

więc dana liczba nie może być kwadratem liczby mniejszej niż 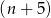(n + 5) . Zatem jedyna możliwość to równość

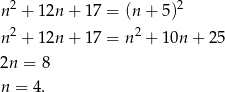
n2 + 12n + 17 = (n+ 5)2 2 2 n + 12n + 17 = n + 10n + 25 2n = 8 n = 4.

Sposób II

Szukamy liczby naturalnej 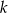k , która spełnia równanie

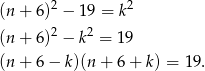
(n + 6)2 − 19 = k2 (n + 6)2 − k2 = 19 (n + 6 − k)(n + 6 + k) = 19 .

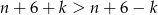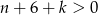Ponieważ obie liczby z lewej strony są liczbami całkowitymi oraz n + 6 + k > n+ 6− k i n+ 6+ k > 0 , jedyna możliwa sytuacja to

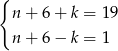
{ n+ 6+ k = 19 n+ 6− k = 1

Dodając te równania stronami mamy

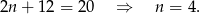
2n + 12 = 20 ⇒ n = 4.

Łatwo sprawdzić, że wtedy

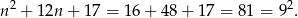
2 2 n + 12n + 17 = 16+ 48+ 17 = 81 = 9 .

 
Odpowiedź: n = 4

Wersja PDF