/Szkoła średnia/Liczby/Potęgi i pierwiastki

Zadanie nr 9551493

Dodaj do ulubionych
Dodaj do rozwiązanych

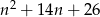Dla jakich liczb naturalnych n , liczba 2 n + 14n + 26 jest kwadratem liczby naturalnej?

Rozwiązanie

Sposób I

Zauważmy, że

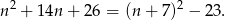
n2 + 14n + 26 = (n+ 7)2 − 23.

To oznacza, że jeżeli liczba ta jest kwadratem liczby naturalnej, to maksymalnie może to być kwadrat liczby 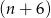(n + 6) . Z drugiej strony,

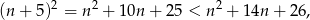
2 2 2 (n+ 5) = n + 10n + 2 5 < n + 14n + 2 6,

więc dana liczba nie może być kwadratem liczby mniejszej niż 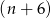(n + 6) . Zatem jedyna możliwość to równość

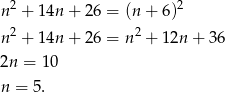
n2 + 14n + 26 = (n+ 6)2 2 2 n + 14n + 26 = n + 12n + 36 2n = 10 n = 5.

Sposób II

Próbujemy znaleźć liczbę naturalną 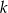k , dla której

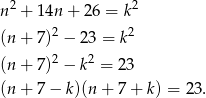
n2 + 14n + 26 = k2 (n + 7)2 − 23 = k2 2 2 (n + 7) − k = 23 (n + 7 − k)(n + 7 + k) = 23 .

Zauważmy, że 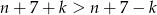n + 7 + k > n + 7− k , więc musimy mieć

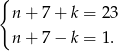
{ n+ 7+ k = 23 n+ 7− k = 1.

Dodając te równania stronami mamy

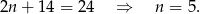
2n + 14 = 24 ⇒ n = 5.

 
Odpowiedź: n = 5

Wersja PDF