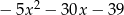Zadanie nr 1467667
Wykres funkcji  przekształcono w symetrii względem prostej
przekształcono w symetrii względem prostej 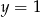 i otrzymano wykres funkcji
i otrzymano wykres funkcji 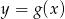 . Wyznacz wzór funkcji
. Wyznacz wzór funkcji 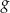 .
.
Rozwiązanie
Zapiszmy daną funkcję w postaci kanonicznej, aby widzieć z jaką parabolą mamy do czynienia
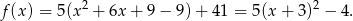
Jest to więc parabola o ramionach skierowanych w górę i wierzchołku w punkcie 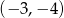 .
.
Sposób I
Odbijając parabolę będącą wykresem funkcji 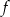 otrzymamy taką samą parabolę, ale z ramionami skierowanymi w dół i wierzchołkiem w punkcie
otrzymamy taką samą parabolę, ale z ramionami skierowanymi w dół i wierzchołkiem w punkcie 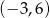 (czyli w punkcie symetrycznym do
(czyli w punkcie symetrycznym do 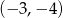 względem prostej
względem prostej 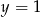 ).
).
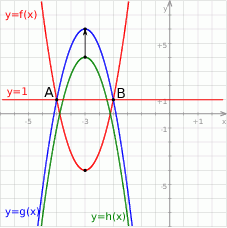
Jest to więc funkcja
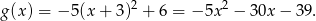
Sposób II
Spróbujmy otrzymać żądany wykres, wykonując kilka prostszych operacji. Najpierw odbijmy wykres funkcji 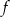 względem osi
względem osi 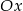 . Otrzymamy w ten sposób wykres funkcji
. Otrzymamy w ten sposób wykres funkcji 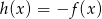 – jest to prawie ten wykres, o który nam chodzi, ale jest odrobinę za nisko – aby otrzymać wykres funkcji
– jest to prawie ten wykres, o który nam chodzi, ale jest odrobinę za nisko – aby otrzymać wykres funkcji 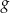 musimy przesunąć wykres
musimy przesunąć wykres 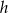 o 2 jednostki do góry. Zatem
o 2 jednostki do góry. Zatem
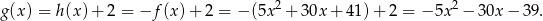
Sposób III
Wyznaczmy punkty wspólne funkcji 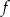 i prostej
i prostej 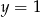 .
.
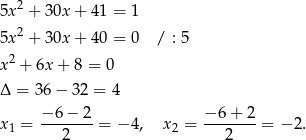
To oznacza, że dana parabola przecina prostą 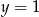 w punktach
w punktach 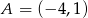 i
i 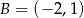 . Parabola odbita względem tej prostej będzie przechodziła przez te same punkty, więc musi mieć postać
. Parabola odbita względem tej prostej będzie przechodziła przez te same punkty, więc musi mieć postać
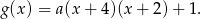
Wiemy ponadto, że ma mieć wierzchołek w punkcie 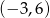 – podstawiamy współrzędne tego punktu, aby obliczyć
– podstawiamy współrzędne tego punktu, aby obliczyć  .
.
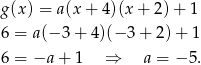
Zatem
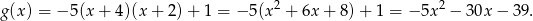
Odpowiedź: