/Szkoła średnia/Funkcje - wykresy/Parabola/Odbicie wykresu

Zadanie nr 2335345

Dodaj do ulubionych
Dodaj do rozwiązanych

Funkcja f określona jest wzorem 2 f(x ) = x + x+ 1 . Znajdź wzór funkcji g , której wykres otrzymamy:

  • przesuwając wykres funkcji o wektor [− 1;− 3] , a następnie otrzymany wykres przekształcając w symetrii względem osi Ox ;
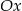  • dokonując obu przekształceń z poprzedniego punktu, ale w odwrotnej kolejności.

Rozwiązanie

Będziemy korzystać ze wzoru na przesunięcie funkcji 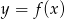y = f(x) o wektor → v = [a,b] :

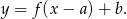
y = f(x − a) + b.
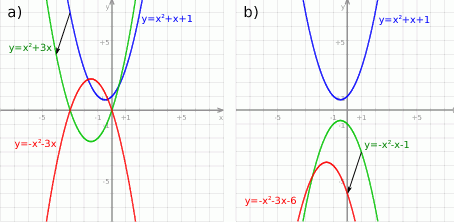
  • Na mocy wspomnianego wzoru, po przesunięciu, mamy funkcję
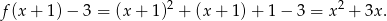
    2 2 f (x + 1)− 3 = (x+ 1) + (x+ 1)+ 1− 3 = x + 3x.

    Przekształcenie wykresu w symetrii względem osi 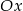Ox zmienia wartości funkcji na przeciwne, otrzymujemy więc funkcję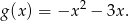

    2 g(x) = −x − 3x .

     
    Odpowiedź: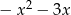 − x2 − 3x

  • Tym razem najpierw odbijamy, czyli mamy wzór 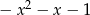− x2 − x− 1 , a potem przesuwamy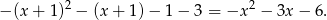
    − (x + 1)2 − (x + 1) − 1− 3 = −x 2 − 3x − 6.

     
    Odpowiedź: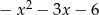 2 − x − 3x − 6

Na koniec obrazek.

PIC
Wersja PDF