Zadanie nr 3282992
Dana jest funkcja 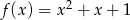 . Napisz wzór funkcji otrzymanej z
. Napisz wzór funkcji otrzymanej z 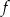 przez
przez
- symetrię względem osi
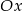 ;
; - symetrię względem osi
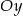 ;
; - symetrię względem punktu
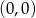 .
.
Rozwiązanie
- Odbicie wykresu względem osi
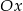 oznacza, że zmieniamy każdą wartość funkcji
oznacza, że zmieniamy każdą wartość funkcji 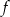 na przeciwną, otrzymamy więc funkcję
na przeciwną, otrzymamy więc funkcję 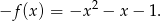
Odpowiedź: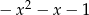
- Odbicie wykresu względem osi
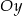 oznacza, że zamieniamy każdy argument funkcji (czyli liczbę, którą do niej wstawiamy) na przeciwną. Otrzymamy więc funkcję
oznacza, że zamieniamy każdy argument funkcji (czyli liczbę, którą do niej wstawiamy) na przeciwną. Otrzymamy więc funkcję 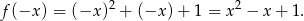
Odpowiedź: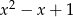
- Odbicie względem punktu
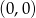 to połączenie (złożenie) poprzednich dwóch odbić – zmieniamy znaki zarówno wartości jak i argumentów. Otrzymamy więc funkcję
to połączenie (złożenie) poprzednich dwóch odbić – zmieniamy znaki zarówno wartości jak i argumentów. Otrzymamy więc funkcję 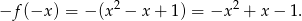
Odpowiedź: